之前使用Java学习过算法的相关实现,也刷过一些题目。现在转Go了,打算用Go再学习一遍,也是对之前不熟悉或者没有遍及到的算法进行一个补充学习。
参考代码随想录:数组理论基础
数组这种数据结构的介绍就不多说了,直接看下面几个LeetCode题目。
代码随想录:
LeetCode 704. 二分查找
这是一道经典的二分查找题目。
二分查找的思路很简单,但是代码写起来却很容易犯错。主要体现在两个方面:
例如到底是 for left < right 还是 for left <= right
到底是right = middle呢,还是要right = middle - 1呢
区分上面两种方法,主要是看区间是怎么定义的。写二分法,区间的定义一般为两种,左闭右闭 即[left, right],或者左闭右开即[left, right)。
这里我们给出左闭右闭 的区间,即:
for left <= rightleft = middle + 1right = middle - 1
如果是左闭右开即[left, right):
for left < rightleft = middle + 1right = middle
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 func search (nums []int , target int ) int left, right := 0 , len (nums)-1 for left <= right { middle := (right + left) / 2 if nums[middle] == target { return middle } else if nums[middle] < target { left = middle + 1 } else { right = middle - 1 } } return -1 }
二分查找相关题目推荐:
这些例题可以参考自己的刷题笔记。
代码随想录:
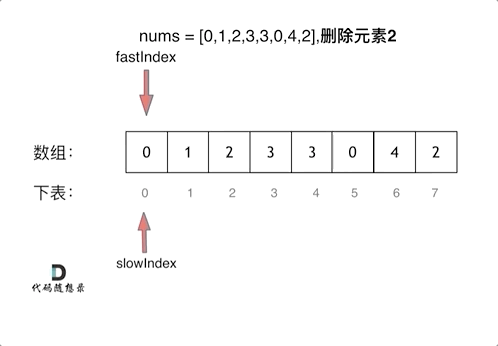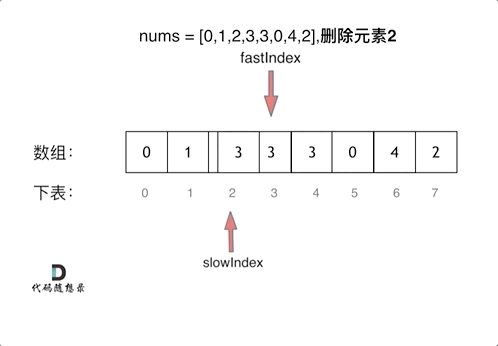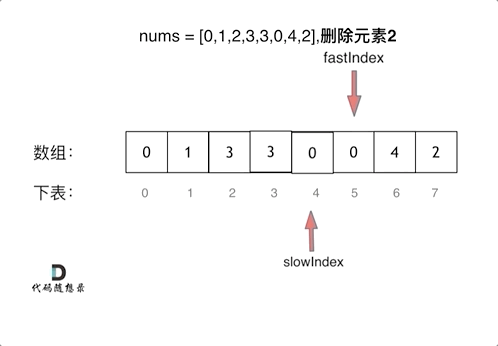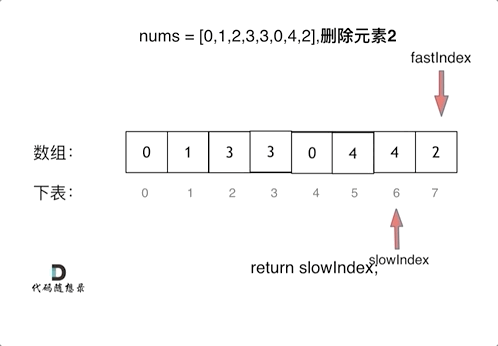
LeetCode 27. 移除元素
定义快慢指针:
快指针:寻找新数组的元素 (新数组就是不含有目标元素的数组)
慢指针:指向更新新数组下标的位置
快指针fast向右遍历旧数组:
如果没有遇到要删除的元素,该元素是新数组的成员。所以将新元素赋值给慢指针slow的位置,并向右移动慢指针slow()
如果遇到了要删除的元素,该元素不是新数组的成员。此时什么都不用做,直接移动快指针fast即可 。(因为不需要更新慢指针slow)
删除过程如下:
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 func removeElement (nums []int , val int ) int length := len (nums) slow, fast := 0 , 0 for fast = 0 ; fast < length; fast++ { if nums[fast] != val { nums[slow] = nums[fast] slow++ } } nums = nums[:slow] return slow }
相关题目推荐:
这些例题可以参考自己的刷题笔记。
代码随想录:
LeetCode 977. 有序数组的平方
方法很简单,将原数组平方处理后直接对新数组排序。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 func sortedSquares (nums []int ) []int for i := range nums { nums[i] = nums[i] * nums[i] } return quicksort(nums) } func quicksort (nums []int ) []int if len (nums) < 2 { return nums } left, right := 0 , len (nums)-1 pivot := 0 nums[pivot], nums[right] = nums[right], nums[pivot] for i := range nums { if nums[i]<nums[right] { nums[left],nums[i] = nums[i],nums[left] left++ } } nums[left],nums[right] = nums[right],nums[left] quicksort(nums[:left]) quicksort(nums[left+1 :]) return nums }
或者直接用Go的sort包。
1 2 3 4 5 6 7 func sortedSquares (nums []int ) []int for i := range nums { nums[i] = nums[i] * nums[i] } sort.Ints(nums) return nums }
**进阶:**请你设计时间复杂度为 O(n) 的算法解决本问题。
官方题解 (方法三)
上面的直接排序,并没有利用数组nums按升序排序 这个条件。
先新建一个答案数组,在遍历过程中依次将结果逆序的放入答案数组中 。我们可以使用两个指针分别指向位置 0 和 n-1,每次比较两个指针对应的数,选择较大的那个逆序 放入答案并移动指针。这种方法无需处理某一指针移动至边界的情况,因为我们是在for i := len(nums) - 1; i >= 0; i--的遍历过程中依次赋值。可以结合代码自行体会。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 func sortedSquares (nums []int ) []int ans := make ([]int , len (nums)) left, right := 0 , len (nums)-1 for i := len (nums) - 1 ; i >= 0 ; i-- { if v, k := nums[left]*nums[left], nums[right]*nums[right]; v < k { ans[i] = k right-- } else { ans[i] = v left++ } } return ans }
时间复杂度:O(n),其中 n 是数组nums 的长度。
空间复杂度:O(1)。除了存储答案的数组以外,我们只需要维护常量空间。
代码随想录:
LeetCode 209. 长度最小的子数组
使用滑动窗口的思想(还是类似双指针)。
使用文字说明可能会看起来更复杂,直接看分析草稿:
这个题解的滑动窗口解法和我想的一样:官方题解
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 func minSubArrayLen (target int , nums []int ) int res := math.MaxInt left := 0 sum := 0 for i, num := range nums { sum = sum + num for sum >= target { res = min(res, i-left+1 ) sum = sum - nums[left] left++ } } if res == math.MaxInt { return 0 } return res } func min (x, y int ) int if x < y { return x } return y }
相关题目推荐:
这些例题可以参考自己的刷题笔记。
代码随想录:
LeetCode 59. 螺旋矩阵 II
参考代码随想录:
按照B站视频的思路,采取左闭右开的区间,转n/2圈,每一圈遍历4条边。具体草稿就不贴了,详细的分析参考视频。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 func generateMatrix (n int ) [][]int if n == 1 { return [][]int {{1 }} } var res [][]int for i := 0 ; i < n; i++ { res = append (res, make ([]int , n)) } count := 1 i, j := 0 , 0 startX, startY := 0 , 0 offset := 1 for k := 0 ; k < n/2 ; k++ { for j = startY; j < n-offset; j++ { res[startX][j] = count count++ } for i = startX; i < n-offset; i++ { res[i][j] = count count++ } for ; j > startY; j-- { res[i][j] = count count++ } for ; i > startX; i-- { res[i][j] = count count++ } startX++ startY++ offset++ j++ } if n%2 != 0 { i++ res[i][j] = count } return res }
但是我在代码随想录的文字版中Golang版本看到了不一样的解法,主要思路是使用left,right来控制横向坐标,使用top,bottom来控制纵向坐标。
具体思路:
初始赋值,left, right := 0, n-1,top, bottom := 0, n-1
第1条边,从左到右,遍历过程为for i := left; i <= right; i++,赋值坐标为[top][i],遍历结束后需要top++(这样就可以准备遍历第2条边了,画一下图就很好理解)
第2条边,从上到下,遍历过程为for i := top; i <= bottom; i++,赋值坐标为[i][right],遍历结束后需要right--
第3条边,从右到左,遍历过程为for i := right; i >= left; i--,赋值坐标为[bottom][i],遍历结束后需要bottom--
第4条边,从下到上,遍历过程为for i := bottom; i >= top; i--,赋值坐标为[i][left],遍历结束后需要left++
至于上述遍历的次数也很好把握,初始赋值count := 1,count最终肯定为n*n,所以只需要在最外层 for count <= n*n即可。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 func generateMatrix (n int ) [][]int res := make ([][]int , 0 ) for i := 0 ; i < n; i++ { res = append (res, make ([]int , n)) } left, right := 0 , n-1 top, bottom := 0 , n-1 count := 1 for count <= n*n { for i := left; i <= right; i++ { res[top][i] = count count++ } top++ for i := top; i <= bottom; i++ { res[i][right] = count count++ } right-- for i := right; i >= left; i-- { res[bottom][i] = count count++ } bottom-- for i := bottom; i >= top; i-- { res[i][left] = count count++ } left++ } return res }
相关题目推荐:
这些例题可以参考自己的刷题笔记。