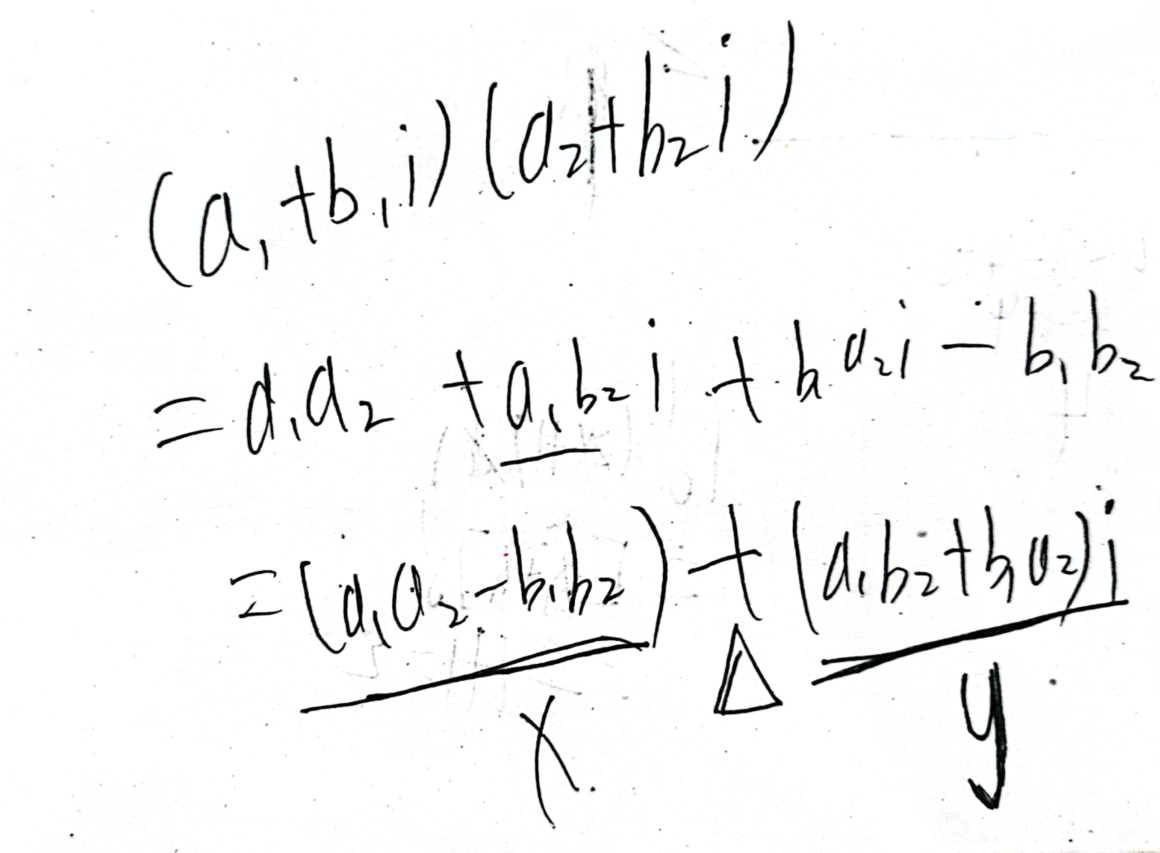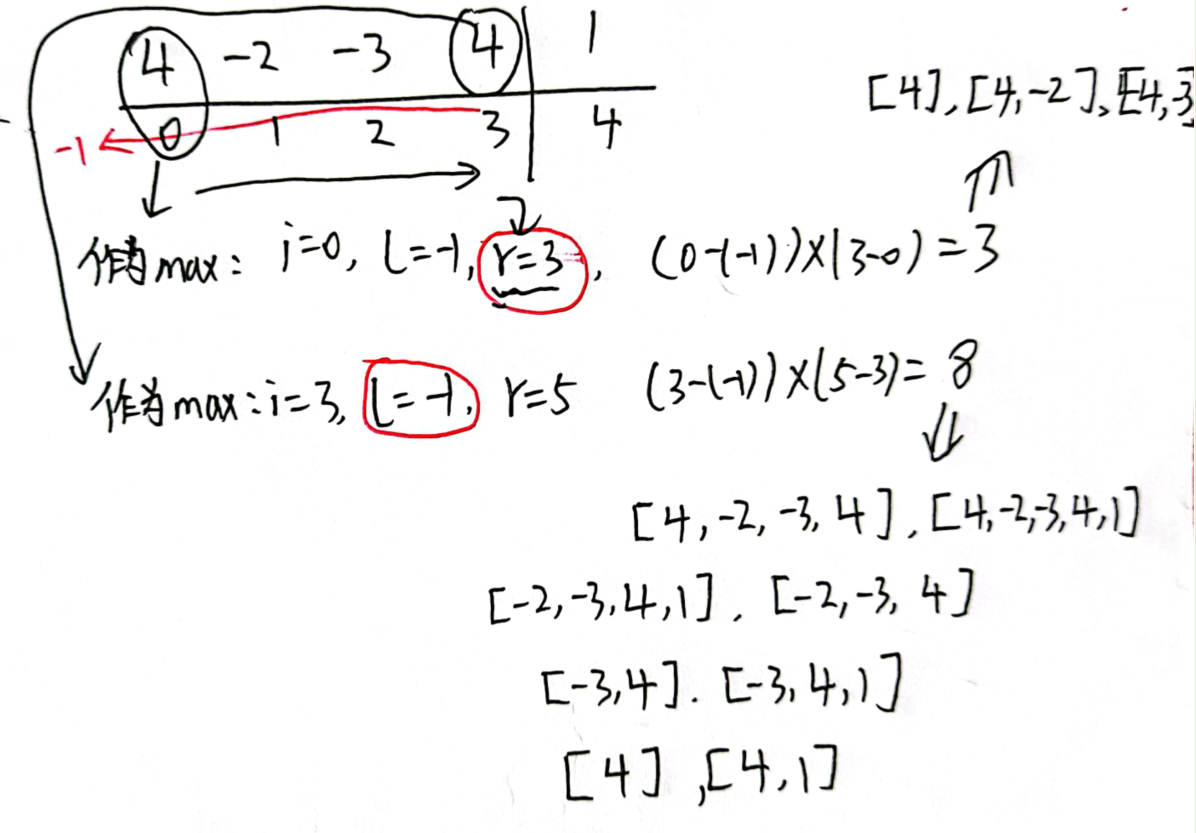LeetCode刷题记录（Java）

1.两数之和

LeetCode 1.两数之和

暴力算法

没啥好说明的。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] result = new int[2];
        for (int i = 0; i < nums.length; i++) {
            int data = target - nums[i];
            for (int j = i+1; j < nums.length; j++) {
                if (data == nums[j]){
                    result[0] = i;
                    result[1] = j;
                    break;
                }
            }
        }
        return result;
    }
}

哈希表

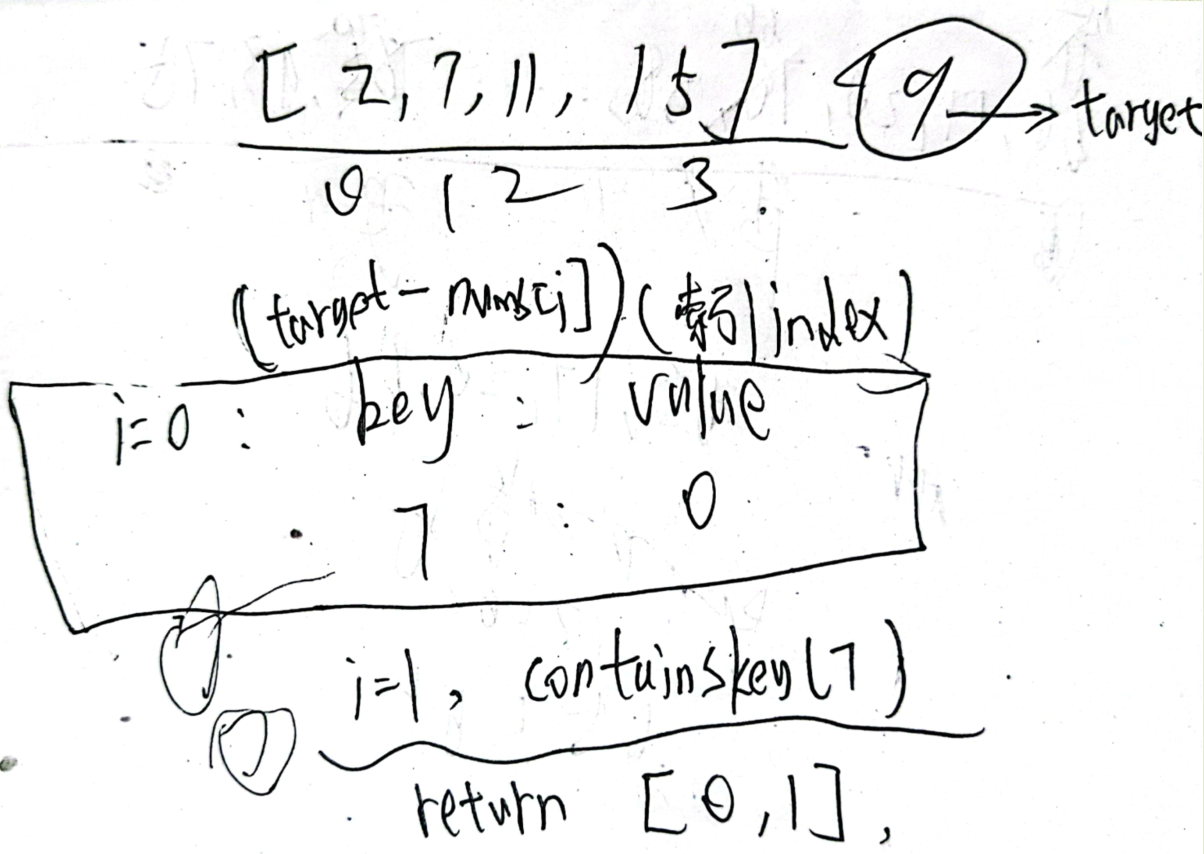
LeetCode第1题，也是我刷的第一题，当时只知道暴力求解。其实用HashMap可以得出时间复杂度为O(n)的解法。

遍历nums数组，在HashMap中，key存储target-nums[i]，value存储索引i。

草稿如下：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer, Integer> map = new HashMap<>();
        int[] ans = new int[2];
        for (int i = 0; i < nums.length; i++) {
            if (map.containsKey(nums[i])){
                ans[0] = map.get(nums[i]);
                ans[1] = i;
                break;
            }
            map.put(target-nums[i], i);
        }
        return ans;
    }
}

2. 两数相加

LeetCode 2. 两数相加

单链表

刚开始看到这题的时候，一看到每位数字都是按照逆序的方式存储的，我就想用栈来讲这些数字拼接成原始的n位数。毕竟栈先进后出的特性，很适合用来实现一些反转效果。

一开始我写的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        Stack<ListNode> stack1 = new Stack<>();
        Stack<ListNode> stack2 = new Stack<>();
        // 将链表1和链表2压入栈
        while (l1!=null){
            stack1.push(l1);
            l1 = l1.next;
        }
        while (l2!=null){
            stack2.push(l2);
            l2 = l2.next;
        }
        // 多次数据类型的转换，看起来很复杂其实实现的目的很单纯
        StringBuilder stringBuilder1 = new StringBuilder();
        StringBuilder stringBuilder2 = new StringBuilder();
        while (!stack1.empty()){
            stringBuilder1.append(stack1.pop().val);
        }
        while (!stack2.empty()){
            stringBuilder2.append(stack2.pop().val);
        }
        String s1 = new String(stringBuilder1);
        String s2 = new String(stringBuilder2);
        // 用Long是为了防止溢出
        Long num1 = Long.valueOf(s1);
        Long num2 = Long.valueOf(s2);
        long sum = num1+num2;
        // 结果的字符串数组，注意结果链表要倒序
        String[] result = Long.toString(sum).split("");
        Stack<ListNode> resultStack = new Stack<>();
        for (String s : result) {   // 字符串已经切割了，所以这里用integer没有问题
            Integer integer = Integer.valueOf(s);
            resultStack.push(new ListNode(integer));
        }
        ListNode head = resultStack.pop();
        ListNode pre = head;
        while (!resultStack.empty()){
            pre.next = resultStack.pop();
            pre = pre.next;
        }
        return head;
    }
}

一开始我用Integer类型接受反转后的数字，提交的时候会有测试用例溢出，后来我用Long类型还是会溢出，这下我就意识到不能一起加，解决这题还是得一位一位的加。

既然要一位一位的加，那就没有必要用到栈了，直接从最低位开始加。需要注意的点有：

  • 在每一位的加法中，注意进位
  • 两个链表的长度可能不一样，所以在代码中的第一个while循环结束后，我新增了两个while循环
  • 运算结束后，最高位可能存在进位，所以我在最后的最后添加了一个if判断

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    private boolean flag = false;    // 是否进位标志
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode dummyNode  = new ListNode();   // 结果链表的头节点
        ListNode pre = dummyNode;
        while (l1!=null&&l2!=null){
            int sum = l1.val + l2.val;
            if (flag){  // 有进位
                sum++;
                flag = false;
            }
            if (sum>=10){
                sum = sum%10;
                flag = true;    // 之后有进位
            }
            pre.next = new ListNode(sum);
            pre = pre.next;
            l1 = l1.next;
            l2 = l2.next;
        }
        // 上一个循环结束后，如果l1和l2的长度不一样，可能还有节点没有加完
        while (l1!=null){
            int sum = l1.val;
            if (flag){  // 有进位
                sum++;
                flag = false;
            }
            if (sum>=10){
                sum = sum%10;
                flag = true;
            }
            pre.next = new ListNode(sum);
            pre = pre.next;
            l1 = l1.next;
        }
        while (l2!=null){
            int sum = l2.val;
            if (flag){  // 有进位
                sum++;
                flag = false;
            }
            if (sum>=10){
                sum = sum%10;
                flag = true;
            }
            pre.next = new ListNode(sum);
            pre = pre.next;
            l2 = l2.next;
        }
        // 最后的最后，如果最后有进位，别忘了+1
        if (flag){
            pre.next = new ListNode(1);
        }
        return dummyNode.next;
    }
}

记录一下LeetCode提交的坑

在最开始，我的flag是这样定义的：private static boolean flag = false;，最后发现在某些测试用例下，执行代码返回结果正确，但提交解答却出错了。这里参考一下LeetCode的文章：

为什么某些测试用例下，执行代码返回结果正确，但提交解答却出错了

果不其然是全局变量的问题，改为private boolean flag = false; 再提交就ok了！

3. 无重复字符的最长子串

LeetCode 3. 无重复字符的最长子串

HashMap

第一次看到这题，我的第一反应使用HashSet。但是后来发现HashSet不能完全满足条件。因为我们遍历的要求是：一旦发现重复值，那么就从前一个重复元素之后的元素开始继续遍历（i = hashMap.get(s.charAt(i));），直到遍历到字符串结尾。

所以选择使用HashMap，其中key存储字符，value存储字符在字符串中的索引。逻辑很简单打下草稿就能看懂。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s.length() == 0) {
            return 0;
        }
        int ans = 0;
        int temp = 0;  // 遍历过程中各个子串的长度
        HashMap<Character, Integer> hashMap = new HashMap<>();
        for (int i = 0; i < s.length(); i++) {
            if (hashMap.containsKey(s.charAt(i))) {
                ans = Math.max(ans, temp);
                temp = 0;
                i = hashMap.get(s.charAt(i));
                hashMap.clear();
            } else {
                hashMap.put(s.charAt(i), i);
                temp++;
            }
        }
        return Math.max(ans, temp);
    }
}

结果为：解答成功:执行耗时:71 ms,击败了13.05% 的Java用户，内存消耗:39.1 MB,击败了8.85% 的Java用户

对哈希表方法的优化：滑动窗口

上面使用HashMap的思路是正确的，但是还可以优化一下。参考powcai大佬提供的题解。

什么是滑动窗口？其实就是一个队列,比如例题中的 abcabcbb，进入这个队列（窗口）为 abc 满足题目要求，当再进入 a，队列变成了 abca，这时候不满足要求。所以，我们要移动这个队列！

如何移动？我们只要把队列的左边的元素移出就行了，直到满足题目要求！一直维持这样的队列，找出队列出现最长的长度时候，求出解！

时间复杂度：O(n)

而这题要求的是最长子串的长度而不是内容，所以我们可以用类似双指针的思想来求出长度，其中left指向子串左边，遍历过程中的i指向子串右边，子串长度即为i-left+1。这样就不用再创建一个双端队列来存储子串了。

  • 首先，判断当前字符是否包含在map中，如果不包含，将该字符添加到map（字符，字符在数组下标），此时没有出现重复的字符，左指针不需要变化。此时不重复子串的长度为：i-left+1，与原来的maxLen比较，取最大值。
  • 如果当前字符 ch 包含在 map中，此时有2类情况：
    • 当前字符包含在当前有效的子段中，如：abca，当我们遍历到第二个a，当前有效最长子段是 abc，我们又遍历到a，那么此时更新 left 为 map.get(a)+1（即我们在上面的方法中分析的，一旦发现重复值，那么就从前一个重复元素之后的元素开始继续遍历），当前有效子段更新为 bca；
    • 当前字符不包含在当前最长有效子段中，如：abba，我们先添加a,b进map，此时left=0，我们再添加b，发现map中包含b，而且b包含在最长有效子段中，我们更新 left=map.get(b)+1（=2），此时子段更新为 b，而且map中仍然包含a，map.get(a)=0；随后，我们遍历到a，发现a包含在map中，且map.get(a)=0，如果我们像1）一样处理，就会发现 left=map.get(a)+1=1，实际上，left此时应该不变，left始终为2，子段变成 ba才对。

感觉这种处理，其实就是，免去了我们之前hashMap.clear();的操作而已。

逻辑打下草稿就很清楚了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s.length() == 0) {
            return 0;
        }
        char[] array = s.toCharArray();
        int ans = 0;
        int left = 0;  // 遍历过程中指向子串左边
        // key为字符，value为该字符在字符串中最后出现的索引（遍历过程中）
        HashMap<Character, Integer> hashMap = new HashMap<>();
        for (int i = 0; i < array.length; i++) {    // 遍历过程中i指向子串右边
            if (hashMap.containsKey(s.charAt(i))){
                // 新的left值取left当前值和重复元素的索引+1这两者之中的最大值
                left = Math.max(left, hashMap.get(array[i])+1);
            }
            hashMap.put(array[i],i);    // 不管是否更新left，都要更新当前遍历字符的位置！
            ans = Math.max(ans, i-left+1);
        }
        return ans;
    }
}

结果为：解答成功:执行耗时:4 ms,击败了87.02% 的Java用户，内存消耗:38.6 MB,击败了41.79% 的Java用户

5. 最长回文子串

LeetCode 5. 最长回文子串

动态规划

虽然还没系统地看过动态规划，但是既然刷到了就试着做一下。

官方题解

创建一个二维布尔数组dp。

在边界条件之内，要判断一个字符串为回文，需要其两端的字符相等且去除两端后的中间字符为回文。可得状态转移方程：dp[l][r] = dp[l+1][r-1]（条件：s[l]==s[r]）。

现在我们来讨论边界条件，分解出来的子问题要构成不了区间，即r-1-(l+1)+1<2，即r-l<3。

边界条件之外的三种情况：

  1. r-l=0，长度为1，肯定是回文，dp[l][r] = true
  2. r-l=1，长度为2，判断两端，相等即为回文
  3. r-l=2，长度为3，判断两端，相等即为回文

边界条件之内才可以使用状态转移方程。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public String longestPalindrome(String s) {
        int length = s.length();
        if (s.length()==1){
            return s;
        }
        int maxLen = 1;    // 记录回文子串最大长度
        int begin = 0;  // 记录回文开始的索引
        // 初始化二维布尔数组dp，dp[l][r]表示s[l]到s[r]之间的字符串是否为回文字符串
        boolean[][] dp = new boolean[length][length];
        for (int i = 0; i < length; i++) {
            dp[i][i] = true;    // l和r相等，字符串长度为1，当然是回文
        }
        for (int r = 1; r < length; r++) {  // 从r开始遍历
            for (int l = 0; l < r; l++) {   // l只需要到r-1即可，因为dp[i][i]已经赋值为true了
                if (s.charAt(l)!=s.charAt(r)){  // 左右两端都不一样，s[l]到s[r]之间不可能是回文
                    dp[l][r] = false;
                }else{  // 左右两端相等的情况
                    if (r-l<3){     // 边界情况，不需要状态转移方程，左右两端相等，直接为true
                        dp[l][r] = true;
                    }else {
                        dp[l][r] = dp[l+1][r-1];
                    }

                    // 只要dp[l][r]为true，即表明s[l]到s[r]之间是回文，需要记录maxLen和begin
                    if (dp[l][r] && r-l+1>maxLen){
                        maxLen = r-l+1;
                        begin = l;
                    }
                }
            }
        }
        return s.substring(begin,begin+maxLen);
    }
}

6. Z 字形变换

LeetCode 6. Z 字形变换

二维矩阵模拟

官方题解

设 length 为字符串 s 的长度，r=numRows。对于特殊情况的处理：

  • s长度为1
  • numRow为1
  • numRows大于等于s的长度

直接返回s即可。

1
2
3
4
// 特殊情况处理（注意还有numRows>=length的情况）
if (length==1 || numRows==1 || numRows>=length){
    return s;
}

根据题意，当我们在矩阵上填写字符时，会向下填写 r 个字符，然后向右上继续填写 r-2 个字符，最后回到第一行。因此 Z 字形变换的周期：t=r+r-2=2r-2。每个周期会占用矩阵上的 1+r-2=r-1 列。

因此我们有 [lengtht]\left[\frac{length}{t}\right] 个周期（向上取整）（最后一个周期视作完整周期），乘上每个周期的列数，得到矩阵的列数 c=[lengtht]⋅(r−1)c=\left[\frac{length}{t}\right] \cdot(r-1) 。

注意这里向上取整的代码处理：int c = (length+t-1)/t * (r-1);

接下来我们就创建一个 r 行 c 列的矩阵，然后遍历字符串 s 并按 Z 字形填写。具体来说，设当前填写的位置为 (x,y)，即矩阵的 x 行 y 列。初始 (x,y)=(0,0)，即矩阵左上角。

若当前字符下标 i ：

  • i%t < r-1。则向下移动
  • 否则，就向上移动

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public String convert(String s, int numRows) {
        int length = s.length();
        // 特殊情况处理（注意还有numRows>=length的情况）
        if (length==1 || numRows==1 || numRows>=length){
            return s;
        }
        int r = numRows;
        int t = 2*r-2;  // 周期
        int c = (length+t-1)/t *(r-1);  // length/t的结果向上取整
        char[][] matrix = new char[r][c]; // 创建矩阵
        int x=0,y=0,i=0;
        while (i<length){
            matrix[x][y] = s.charAt(i);
            if (i%t < r-1){ // 向下移动
                x++;
            }else { // 想右上方移动
                x--;
                y++;
            }
            i++;
        }
        StringBuilder ans = new StringBuilder();
        for (char[] chars : matrix) {
            for (char aChar : chars) {
                if (aChar != 0){    // 注意这里是不等于0!!!
                    ans.append(aChar);
                }
            }
        }
        return ans.toString();
    }
}

复杂度分析：

  • 时间复杂度：O(r*n)。其中 r*=*numRows，n 为字符串 s 的长度。
  • 空间复杂度：O(r*n)。矩阵需要O(r*n)的空间。

7. 整数反转

LeetCode 7. 整数反转

数学

一开始我写的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public int reverse(int x) {
        if (x < 10 && x > -10) {
            return x;
        }
        String str = String.valueOf(x);
        char[] arr = str.toCharArray();
        if (x > 0) {
            // 双指针实现反转，已经很熟悉了
            int l = 0;
            int r = arr.length - 1;
            while (l < r) {
                char temp = arr[l];
                arr[l] = arr[r];
                arr[r] = temp;
                l++;
                r--;
            }
        } else { // x为负数
            // 双指针实现反转，已经很熟悉了
            int l = 1;
            int r = arr.length - 1;
            while (l < r) {
                char temp = arr[l];
                arr[l] = arr[r];
                arr[r] = temp;
                l++;
                r--;
            }
        }
        StringBuilder ans = new StringBuilder();
        boolean flag = true;    // 还没有处理前置位为0的情况
        for (char c : arr) {
            if (c=='0' && flag){    // 处理前置位为0的情况
                flag = false;
                continue;
            }
            ans.append(c);
        }
        return Integer.parseInt(ans.toString());
    }
}

但是在跑测试用例：9646324351时，会报错9646324351 is not a valid value of type integer

所以还是不可以简单的先转字符串反转再转int。

官方题解

记 rev 为翻转后的数字，为完成翻转，我们可以重复弹出 x 的末尾数字，将其推入 rev 的末尾，直至 x 为 0。

要在没有辅助栈或数组的帮助下弹出和推入数字，我们可以使用如下数学方法：

1
2
3
4
5
// 弹出 x 的末尾数字 digit
digit = x % 10
x = x/10
// 将数字 digit 推入 rev 末尾
rev = rev * 10 + digit

草稿如下：

（该方法对负数同样有效。在Java中：-7%10=-7；-7/10=0；-12%10=-2；-12/10=-1）

确定了通过数学处理来实现反转之后，接下来只需要注意溢出即可。

根据题目要求，我们需要在推入数字之前，判断是否满足：$$
-2^{31} \leq \text { rev } \cdot 10+\text { digit } \leq 2^{31}-1

，若该不等式不成立则返回0。但是∗∗题目要求不允许使用64位整数∗∗，即运算过程中的数字必须在32位有符号整数的范围内，因此我们不能直接按照上述式子计算，需要进行处理：>判断不等式>，若该不等式不成立则返回 0。 但是**题目要求不允许使用 64 位整数**，即运算过程中的数字必须在 32 位有符号整数的范围内，因此我们不能直接按照上述式子计算，需要进行处理： > 判断不等式 >

-2^{31} \leq \text { rev } \cdot 10+\text { digit } \leq 2^{31}-1

是否成立，可改为判断不等式、是否成立，可改为判断不等式、

\left\lceil\frac{-2^{31}}{10}\right\rceil \leq r e v \leq\left\lfloor\frac{2^{31}-1}{10}\right\rfloor

详细数学推论可以参考[官方题解](https://leetcode−cn.com/problems/reverse−integer/)详细数学推论可以参考[官方题解](https://leetcode-cn.com/problems/reverse-integer/)

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int reverse(int x) {
        if (x < 10 && x > -10) {
            return x;
        }
        int rev = 0;
        int digit = 0;
        while (x!=0){
            if (rev>Integer.MAX_VALUE/10 || rev<Integer.MIN_VALUE/10){  // 溢出
                return 0;
            }
            digit = x % 10;
            x = x/10;
            rev = rev*10 + digit;
        }
        return rev;
    }
}

9. 回文数

LeetCode 9. 回文数

双指针

首先对特殊情况的处理：x为负数则一定返回false。

然后将num转换成char数组，使用双指针遍历即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean isPalindrome(int x) {
        if (x<0){   // 特殊情况处理
            return false;
        }
        char[] arr = String.valueOf(x).toCharArray();
        int l = 0;
        int r = arr.length-1;
        while (l<r){
            if (arr[l]!=arr[r]){
                return false;
            }
            l++;
            r--;
        }
        return true;
    }
}

11.盛最多的水的容器

LeetCode 11.盛最多水的容器

贪心算法

说明：贪心算法的思想体现在左右边界的移动上，首先取最左边和最右边为边界。然后判断哪边的高小，哪边的边界就移动。（因为移动之后低就变小了，只有找到更大的高，才有可能找到更优的解）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int maxArea(int[] height) {
        int left = 0;
        int right = height.length - 1;
        int res = 0;    // 最大结果
        int temp = 0;    // 暂存体积
        while (left<right){     // 循环条件即左边界要小于右边界
            temp = Math.min(height[left],height[right])*(right - left); // 取较短的那一段为高，很好理解（盛水）
            res = Math.max(temp,res);
            /**
             * 这里就开始体现到贪心算法而不是简单的暴力算法
             * 哪边低，移动哪边的边界
             */
            if (height[left]<height[right]){    // 如果左边界的高小，则左边界的指针右移，去遍历看看有没有更优解
                left++;
            }else { // 右边界高小，右边界左移一段
                right--;
            }
        }
        return res;
    }
}

方法：贪心算法+双指针
本题虽然用到了双指针作为辅助，但关键还是要有贪心的思想，循环每一种可能出现最优的结果（而不是简单的暴力遍历），不断保存局部最优解，等到循环结束的时候就是全局最优解，时间复杂度为O(n)，空间复杂度为O(1)

本题用到的贪心思想的理解就是在循环的过程中，每次让较短的一端移动来更新res的最大值，比之前的值大就更新最大值，等到循环结束，其最终更新的值就是全局最优解。时间复杂度为O(n)，空间复杂度为O(1)

此题也可以说是dp问题，都有最优子结构，主要原因是贪心是特殊的动态规划。 补充：

  • 动态规划具有两个性质：重叠子问题和最优子结构
  • 贪心算法：贪心选择性质和最优子结构

最优子结构性质是指问题的最优解包含其子问题的最优解时，就称该问题具有最优子结构性质，重叠子问题指的是子问题可能被多次用到， 多次计算，动态规划就是为了消除其重叠子问题而设计的。其实贪心算法是一种特殊的动态规划，由于其具有贪心选择性质，保证了子问题只会被计算一次，不会被多次计算，因此贪心算法其实是最简单的动态规划。

14. 最长公共前缀

LeetCode 14. 最长公共前缀

19. 删除链表的倒数第 N 个结点

LeetCode 19. 删除链表的倒数第 N 个结点

单链表

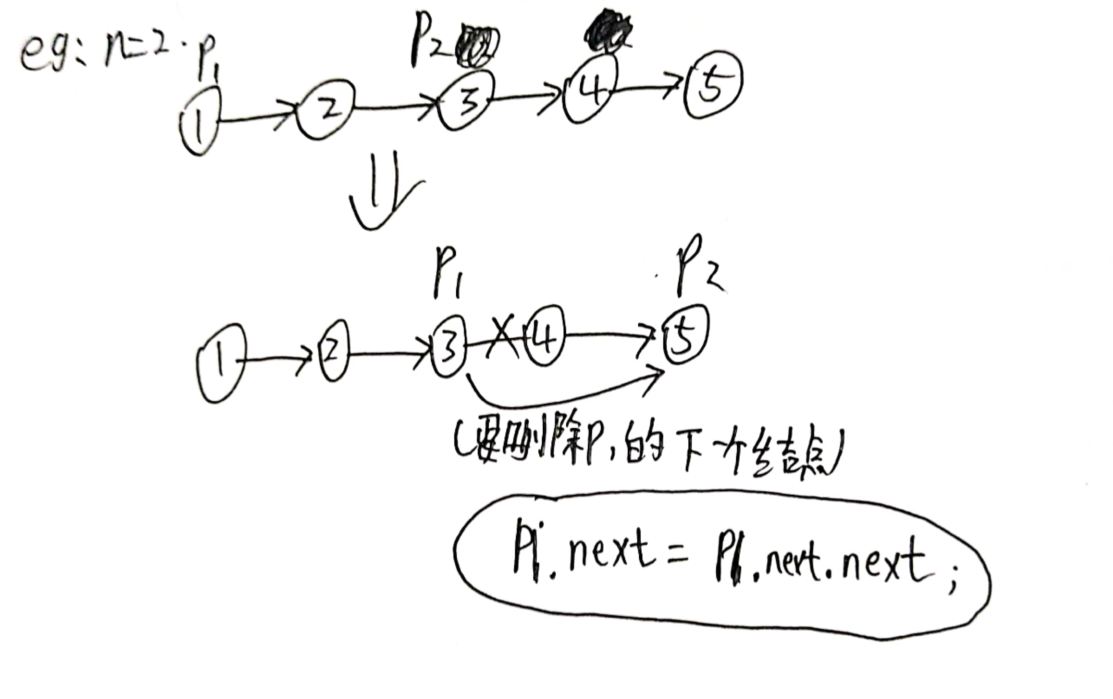
这题在之前数据结构笔记中的链表实现部分中已经写过了，这里再说一下实现思路。

定义两个指针p1和p2，其中p2比p1快n个结点。这样当p2结点走到链表的最后一个时，我们要删除的倒数第n个结点即为p1指向的下一个结点，删除逻辑就很好实现了。这里要注意一个特殊情况：当n和链表长度一样时，在实现p2比p1快n个结点的循环体中会出现p2.next为null的空指针异常。这时由于n和链表长度一样，我们删除链表的第一个结点即可。代码体现在：

1
2
3
4
5
6
7
for (int i = 0; i < n; i++) {
    // 特殊情况：链表结点数和n相同，会在循环的最后一步中出现p2.next为null,而当链表结点数和n相同时，即删除第1个节点
    if (p2.next==null){
        return head.next;   // 删除链表中第一个结点
    }
    p2 = p2.next;
}

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        /* 定义两个指针p1和p2，其中p2比p1快n个结点 */
        ListNode p1 = head;
        ListNode p2 = head;
        for (int i = 0; i < n; i++) {
            // 特殊情况：链表结点数和n相同，会在循环的最后一步中出现p2.next为null,而当链表结点数和n相同时，即删除第1个节点
            if (p2.next==null){
                return head.next;   // 删除链表中第一个结点
            }
            p2 = p2.next;
        }
        while (p2.next!=null){
            p1 = p1.next;
            p2 = p2.next;
        }
        // 循环结束后p2指向最后一个结点，要删除的结点即为p1的下一个结点
        p1.next = p1.next.next;
        return head;
    }
}

20. 有效的括号

20. 有效的括号

栈

分析：这题是LeetCode上的简单题，我的思路是用栈来解决。用文字说明比较麻烦，直接上图吧，过程中注意一下图中逻辑要在栈的长度大于等于2的情况下。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public boolean isValid(String s) {
        // 将字符串变成字符数组
        char[] array = s.toCharArray();
        Stack<Character> stack = new Stack<>();
        stack.push(array[0]);   // 先将第一个字符push到栈中
        for (int i = 1; i < array.length; i++) {
            stack.push(array[i]);
            // 在测试用例"()[]{}"中，如果不加以判断会存在栈的长度不足2的情况
            if (stack.size()>=2){   // stack长度在大于等于2才能执行以下逻辑
                Character pop = stack.pop();
                Character peek = stack.peek();
                // 判断pop和peek(即栈的前两个元素)是不是能组成有效括号
                // 能组成有效括号的无非就三种情况，这里注意下pop后面的括号，peek是前面的括号即可
                if ( (pop==')'&&peek=='(') || (pop==']'&&peek=='[') || (pop=='}'&&peek=='{') ){
                    stack.pop();    // 将原本peek的也pop出栈
                }else { // pop和peek没有形成有效括号，记得pop要push回栈中
                    stack.push(pop);
                }
            }
        }
        return stack.empty(); // 栈为空，说明是有效括号
    }
}

结果为：解答成功:执行耗时:2 ms,击败了56.70% 的Java用户,内存消耗:36.6 MB,击败了38.71% 的Java用户

这里我自己写的代码运行时间为2ms，我看到也有人用栈来实现，但是只花了1ms。思路大概是一样的，但是对我最开始写的代码进行了许多优化（具体体现在可以提前判断不可能是有效括号，直接返回false。提前返回false：在迭代过程中，提前发现不符合的括号并且返回，提升算法效率）。

判断提前返回false的重点在于右括号：当向栈中插入右括号时，一定要随时判断能否形成有效括号，若不能则直接返回false。我们在用栈来处理这个问题时，只要一出现右括号，其前一个括号必须要与之形成有效括号，否则就返回false。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (c=='('||c=='['||c=='{'){    // 是左括号，直接push
                stack.push(c);
            }else {
                // 如果是右括号，且栈已经是空了(插入的右括号在栈底，那么就永远不会出现有效括号与其匹配，直接return false)
                if (stack.empty()){
                    return false;
                }else { // 下面的判断是对右括号但没有返回false的情况（即是右括号且栈不为空）
                    Character pop = stack.pop();
                    if (c==')'){
                        if (pop!='('){
                            return false;
                        }
                    }else if (c==']'){
                        if (pop!='['){
                            return false;
                        }
                    }else if (c=='}'){
                        if (pop!='{'){
                            return false;
                        }
                    }
                }
                }
            }
        return stack.empty(); // 栈为空，说明是有效括号
    }
}

结果为：解答成功:执行耗时:1 ms,击败了98.94% 的Java用户,内存消耗:36.2 MB,击败了92.51% 的Java用户

21. 合并两个有序链表

LeetCode 21. 合并两个有序链表

双指针

这题跟LeetCode 88. 合并两个有序数组思路挺像的，都可以用双指针来实现。

思路很清晰，打个草稿就可以了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode dummyNode = new ListNode();
        ListNode p = dummyNode;
        ListNode p1 = list1;
        ListNode p2 = list2;
        while (p1!=null && p2!=null){
            if (p1.val<p2.val){
                p.next = p1;
                p1 = p1.next;
                p = p.next;
            }else {
                p.next = p2;
                p2 = p2.next;
                p = p.next;
            }
        }
        // 上个循环结束后，可能还有链表没有走完
        while (p1!=null){
            p.next = p1;
            p1 = p1.next;
            p = p.next;
        }
        while (p2!=null){
            p.next = p2;
            p2 = p2.next;
            p = p.next;
        }
        return dummyNode.next;
    }
}

22. 括号生成

LeetCode 22. 括号生成

回溯+剪枝

参考liweiwei1419大佬的题解。

这一类问题是在一棵隐式的树上求解，可以用深度优先遍历，也可以用广度优先遍历。
一般用深度优先遍历。原因是：

  • 代码好写，使用递归的方法，直接借助系统栈完成状态的转移；
  • 广度优先遍历得自己编写结点类和借助队列。

首先我们要知道，有效的括号，从左到右依次遍历下来，左括号的数量一定严格大于等于右括号，即(的个数一定严格大于等于)。

以n=2为例：

根据上面的分析以及图，可以得出以下结论：

  • 当前左右括号都可以使用的时候，即左右括号剩余数量大于0，才产生分支；
  • 产生左分支的时候，只看当前是否还有左括号可以使用，即左括号剩余数量大于0；
  • 产生右分支的时候，还受到左分支的限制，左括号的数量一定严格大于等于右括号的时候，才可以产生分支；
  • 在左括号和右括号剩余数量都等于0的时候结算。

总之一句话：在遍历过程中，无效的括号即是出现了左括号小于右括号的情况。这就是我们要剪枝的。

回溯算法的代码中，为了方便理解，可以将return理解为回溯到上一步。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    private List<String> result  = new ArrayList<>();
    public List<String> generateParenthesis(int n) {
        if (n==0){
            return result;
        }
        StringBuilder path = new StringBuilder();   // 回溯过程中生成的字符串
        dfs(path,0,0,n);
        return result;
    }

    /**
     * @param path
     * @param left 左括号使用数量
     * @param right 左括号使用数量
     * @param n 给定的n值，即左右括号数量
     */
    private void dfs(StringBuilder path, int left, int right, int n) {
        // 左右括号都用完了，到达叶子结点了，将结果添加到result中，然后回溯到上一步
        if (left==n&&right==n){
            result.add(path.toString());
            return;
        }
        // 剪枝（剪掉无效的括号，即已经使用的左括号left<已经使用的右括号right）
        if (left<right){
            return;     // 回溯到上一步
        }
        // 产生分支
        if (left<n){    // 产生左分支
            path.append("(");
            dfs(path, left+1, right, n);    // 使用了左括号，left+1
            path.deleteCharAt(path.length()-1);   // 每一个dfs执行完后，即当前结点已经无路可走了，回溯到上一个结点，别忘了要删除path的最后一个括号
        }

        if (right<n){    // 产生右分支
            path.append(")");
            dfs(path, left, right+1, n);    // 使用了右括号，right+1
            path.deleteCharAt(path.length()-1);   // 每一个dfs执行完后，即当前结点已经无路可走了，回溯到上一个结点，别忘了要删除path的最后一个括号
        }
    }
}

在第一次学习回溯法的时候，代码看下来是很懵的。但是结合这个代码并且在IDE中进行debug，我有了自己的理解：

  • 递归过程中dfs()函数的每一次调用，都可以理解为向下生成结点
  • 在生成分支的代码部分，每次dfs()函数执行完后，都会删除path的最后一个字符，这里就体现到回溯了，回溯到上一个结点，如果能继续产生分支的话，就继续向下生成结点；不能生成分支了，就继续向上回溯到上一个dfs()函数，同时删除path的最后一个字符。（这里的逻辑可以一边debug一边画剪枝树，体现到了深度优先搜索的思想）
  • return也可以理解为回溯到上一步，因此代码中有3中情况需要回溯：
    • 该结点所有能走的路已经全部走完了，回溯到上一个结点（具体体现在每一个dfs()函数执行完后，都会删除path的最后一个括号。这里回溯到上一个结点，即执行上一个dfs()函数，完全是通过递归实现的）
    • 该结点是叶子结点，记录结果后回溯到上一个结点（具体体现在add之后就return了）
    • 该结点不满足我们分析的条件（即不能保证是有效括号），需要剪枝掉该结点，然后回溯到上一个结点（具体体现在我们判断出left<right后，直接return）

这是我当时一边debug一边打的草稿，很潦草但是我不想再画一次了，不懂的话可以一边debug一边再画一下，很好理解的。

30. 串联所有单词的子串

LeetCode 30. 串联所有单词的子串

哈希表+子数组匹配

视频讲解

首先要注意题目给出的关键信息：单词数组words中的各个单词长度相同。

这题我们通过HashMap，将字符串s转换为对应的数组，然后根据子数组匹配问题的相关算法，完成本题。

在转换words时，list存储各个子串出现的次数。但是我们不知道list中各个索引处的值表示的是哪个子串出现的次数，所以我们还需要使用HashMap。map的key是子串，value存储ist中的一个l索引，可以通过该索引和list查出该子串出现的次数。最后我们再将list转换成数组times。这时我们就将words数组转换成一个int数组times了，其中words数组的各个子串被映射到了times数组的各个索引。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
    public List<Integer> findSubstring(String s, String[] words) {
        int w_len = words.length;   // words数组长度（一维）

        HashMap<String, Integer> map = new HashMap<>(); // 注意map的value存储的是索引（list中的）
        // 将words转换为times数组
        List<Integer> list = new ArrayList<>(); // 存储子串出现次数
        int index = 0;
        for (String word : words) {
            if (map.containsKey(word)) { // 该子串已经出现过了，那么更新list即可
                Integer value_index = map.get(word);
                list.set(value_index, list.get(value_index) + 1);  // 在value_index索引处更新list
            } else {  // 首先更新map，其次将新的子串出现的次数添加到list中
                map.put(word, index++);
                list.add(1);
            }
        }
        // list转换为一个times数组
        int[] times = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            times[i] = list.get(i);
        }

        // 字符串s转为为数组,并进行子数组匹配算法
        int size = words[0].length();   // words数组中字符串长度（二维）
        List<Integer> out = new ArrayList<>(); //
        for (int i = 0; i < size; i++) {
            List<Integer> keep = new ArrayList<>(); //
            for (int j = i+size; j <= s.length(); j+=size) {   // 每次采样size个单词
                keep.add(map.getOrDefault(s.substring(j-size,j),-1));
            }
            // 子数组匹配
            // 先定义两个指针
            int p1 = 0;
            int p2 = 0;
            int[] rest = times.clone();
            while (p2< keep.size()){
                if (keep.get(p2)==-1){
                    p2++;
                    p1=p2;
                    rest = times.clone();   // 复原rest
                }else {
                    int index2 = keep.get(p2);
                    while (rest[index2]==0){
                        rest[keep.get(p1++)]++;
                    }
                    rest[index2]--;
                    p2++;
                    if (p2-p1 == words.length){
                        out.add(p1*size+i);
                    }
                }
            }
        }
        return out;
    }
}

36. 有效的数独

LeetCode 36. 有效的数独

哈希表

参考三叶大佬题解。

使用 哈希表 来记录某行/某列/某个区域出现过哪些数字，来帮助我们判断是否符合有效数独的定义。这样我们去遍历i行j列即可。

使用哈希表比较麻烦的地方就在如何根据给定i和j来确定3x3区域的编号id_area。

可以推导出如下关系：id_area = (i/3)*3 + j/3;

因此在i行j列的遍历过程中：

  • 如果第i行出现重复数字，return false；
  • 如果第j列出现重复数字，return false；
  • 如果第id_area个区域出现重复数字，return false；

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    int count;
    public boolean isValidSudoku(char[][] board) {
        Map<Integer, HashSet<Character>> row = new HashMap<>(); // 检测每一行是否合法
        Map<Integer, HashSet<Character>> col = new HashMap<>(); // 检测每一列是否合法
        Map<Integer, HashSet<Character>> area = new HashMap<>(); // 检测每个3x3区域是否合法
        // 初始化每一个需要检测区域的HashSet
        for (int i = 0; i < 9; i++) {
            row.put(i, new HashSet<>());
            col.put(i, new HashSet<>());
            area.put(i, new HashSet<>());
        }
        // 开始遍历数独，往HashSet中存储数据
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j]=='.'){  // 不是数字，不用往HashSet中存储，因为规则只是1-9的数字只能出现一次
                    continue;
                }
                int id_area = (i/3)*3 + j/3;
                // 如果第i行或第j列或第id_area个3x3区域存在重复数字，即为不合法数独
                if (row.get(i).contains(board[i][j]) || col.get(j).contains(board[i][j]) || area.get(id_area).contains(board[i][j]) ){
                    return false;
                }
                row.get(i).add(board[i][j]);
                col.get(j).add(board[i][j]);
                area.get(id_area).add(board[i][j]); // 注意这里是id_area
            }
        }
        return true;
    }
}

复杂度分析：

  • 时间复杂度：在固定 9*9 的问题里，计算量不随数据变化而变化。复杂度为 O(1)。
  • 空间复杂度：在固定 9*9 的问题里，存储空间不随数据变化而变化。复杂度为 O(1)。

数组

同样是参考三叶大佬题解。

大多数的哈希表计数问题，都能转换为使用数组解决。

虽然时间复杂度一样，但哈希表的更新和查询复杂度为均摊 O(1)，而定长数组的的更新和查询复杂度则是严格 O(1)。

因此从执行效率上来说，数组要比哈希表快上不少。

思路比较清晰，举个例子：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    int count;
    public boolean isValidSudoku(char[][] board) {
        boolean[][] rol = new boolean[10][10];
        boolean[][] col = new boolean[10][10];
        boolean[][] area = new boolean[10][10];
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                char c = board[i][j];
                if (c=='.'){
                    continue;
                }
                int value = c - '0';
                if (rol[i][value] || col[j][value] || area[(i/3)*3 + j/3][value]){
                    return false;
                }
                rol[i][value] = true;
                col[j][value] = true;
                area[(i/3)*3 + j/3][value] = true;
            }
        }
        return true;
    }
}

42. 接雨水

LeetCode 42. 接雨水

单调栈

这道题目可以用单调栈来做。单调栈就是比普通的栈多一个性质，即维护一个栈内元素单调。

单调栈O(n)解决，动图预警

官方题解

上面大佬提供的题解已经说的非常清楚了，这里我用自己的语言理解一下。

注意：单调栈中存放的不是高度本身，而是其在height数组中的索引。（这种处理已经很熟悉了，在[739. 每日温度](#739. 每日温度)中也是这么处理的）

从左到右遍历height数组，遍历到下标 i 时，如果栈内至少有两个元素，记栈顶元素为 top，top的下面一个元素是 left，则一定有height[left]>=height[top]（因为我们会保证其是单调栈），如果height[i]>height[top]，则得到一个可以接雨水的区域（同时为了保证单调栈我们会将top元素push出栈），该区域的宽度是i-left-1，高度是Math.min(height[i], height[left]) - height[top]。得出高度和宽度之后，就可以计算出能接到的水了。

这么理解：要能接到水，必须得是凹结构，即高-低-高。在我们遍历的过程中，left元素即为左边柱子，i即为右边柱子（因为height[i]>height[top]所以能接到水），top即为中间最低的柱子。所以我们在计算宽度时与top无关的，宽度为：i-left-1；但是在计算高度时就与top有关了，高度为：Math.min(height[i], height[left]) - height[top]（这个非常好理解，因为求能接水的高度肯定是左右两边最矮的减去中间的高度）（画一下图应该就能理解了）

这样就好理解多了，因此，为了保证能够接到水，我们必须要保证有三个柱子（元素），因此栈中元素至少要有两个我们才能计算能接到的水。所以在while循环下会有这么一段代码：

1
2
3
4
5
6
7
8
9
10
11
12
    // for循环遍历数组
    for (int i = 0; i < height.length; i++) {
        // while循环保证单调栈，同时计算结果
        while (!stack.isEmpty() && height[i]> height[stack.getLast()]){
            Integer top = stack.removeLast();
            if (stack.isEmpty()){   // 保证栈中至少有两个元素（高-低-高结构才能接水）
                break;
            }
……
        }
        stack.addLast(i);
    }

for循环遍历结束后，栈中剩下的柱子（元素）无法再出现高-低-高的情况，所以不会再接到水，我们无需处理。

代码大体框架同[739. 每日温度](#739. 每日温度)中一样的：for循环开始遍历height数组，for循环下面还有一个while循环来保证栈是单调栈同时计算接到的雨水。while循环结束后即将当前遍历的内容push到栈中。

其他的细节上面的题解以及提供的gif已经很清晰了，这里搬运一张gif：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int trap(int[] height) {
        ArrayDeque<Integer> stack = new ArrayDeque<>(); // 单调栈
        int result = 0;     // 结果
        // for循环遍历数组
        for (int i = 0; i < height.length; i++) {
            // while循环保证单调栈，同时计算结果
            while (!stack.isEmpty() && height[i]> height[stack.getLast()]){
                Integer top = stack.removeLast();
                if (stack.isEmpty()){   // 保证栈中至少有两个元素（高-低-高结构才能接水）
                    break;
                }
                int w = i - stack.getLast() - 1;    // 接水宽度
                int h = Math.min(height[stack.getLast()], height[i]) - height[top]; // 接水高度
                result = result + h*w;
            }
            stack.addLast(i);
        }
        return result;
    }
}
  • 时间复杂度：O(n)。其中n是数组height的长度。从 0到 n-1的每个下标最多只会入栈和出栈各一次
  • 空间复杂度：O(n)。其中n是数组height的长度。空间复杂度主要取决于栈空间，栈的大小不会超过 n

43. 字符串相乘

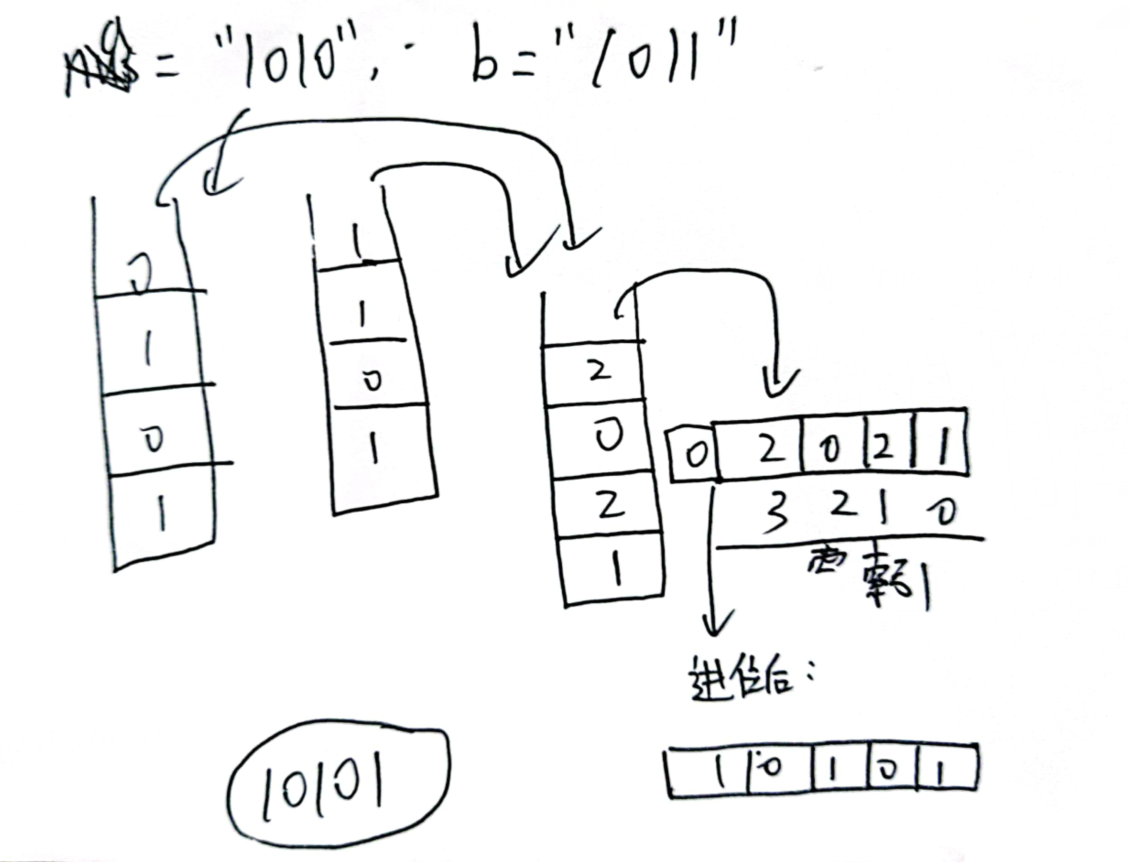
LeetCode 43. 字符串相乘

模拟

官方题解

这里我们使用数组代替字符串来存储结果，则可以减少对字符串的操作。

数学知识：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public String multiply(String num1, String num2) {
        // 特殊情况处理
        if (num1.equals("0") || num2.equals("0")){
            return "0";
        }

        int m = num1.length();
        int n = num2.length();
        int[] ansArr = new int[m + n];
        for (int i = m-1; i >= 0; i--) {
            int x = num1.charAt(i) - '0';
            for (int j = n-1; j >= 0; j--) {
                int y = num2.charAt(j) - '0';
                ansArr[i+j+1] = ansArr[i+j+1]+(x*y);
            }
        }
        // 处理进位
        for (int i = m + n - 1; i > 0; i--) {
            ansArr[i-1] = ansArr[i-1]+(ansArr[i]/10);
            ansArr[i] = ansArr[i]%10;
        }
        // 处理首位为0的情况
        int index = ansArr[0]==0? 1:0;  // 使用三元表达式更加简便
        StringBuilder ans = new StringBuilder();
        for (int i = index; i < m+n; i++) {
            ans.append(ansArr[i]);
        }
        return ans.toString();
    }
}

45. 跳跃游戏 II

LeetCode 45. 跳跃游戏 II

贪心算法

这个的贪心思想有点绕，视频讲解。

分析：相较于55.跳跃游戏，这题是两步贪心。55.跳跃游戏只需要一步贪心——即根据当前下标i能跳到的最远下标farthest进行贪心选择。但是这题却需要两步贪心，不仅需要当前下标i能跳到的最远下标currentMax，还需要考虑，从当前下标i跳到下一个下标i2后，从i2开始能够到达的最远下标nextMax。我们需要在这两步贪心中，找到需要跳跃的下标i并更新i，同时跳跃数steps++。最后返回steps。

我们「贪心」地进行正向查找，每次找到可到达的最远位置，就可以在线性时间内得到最少的跳跃次数。

例如，对于数组 [2,3,1,2,4,2,3]，初始位置是下标 0，从下标 0 出发，最远可到达下标 2。下标 0 可到达的位置中，下标 1 的值是 3，从下标 1 出发可以达到更远的位置（nextMax为4），因此第一步到达下标 1。

从下标 1 出发，最远可到达下标 4。下标 1 可到达的位置中，下标 4 的值是 4 ，从下标 4 出发可以达到更远的位置，因此第二步到达下标 4。

在具体的实现中，我们维护当前能够到达的最大下标位置，记为currentMax。我们从左到右遍历数组，到达currentMax时，更新currentMax并将跳跃数steps+1。

在遍历数组时，我们不访问最后一个元素，这是因为在访问最后一个元素之前，我们的currentMax一定大于等于最后一个位置，否则就无法跳到最后一个位置了。如果访问最后一个元素，在边界正好为最后一个位置的情况下，我们会增加一次「不必要的跳跃次数」，因此我们不必访问最后一个元素。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int jump(int[] nums) {
        int length = nums.length;   // 数组长度
        int steps = 0;    // 跳跃次数
        int currentMax = 0;     // 当前下标i能到达的最远下标
        int nextMax = 0;        // 从当前下标i跳到下一个下标i2后，从i2开始能够到达的最远下标
        for (int i = 0; i < length - 1; i++) {
            nextMax = Math.max(nextMax, i+nums[i]);
            if (i==currentMax){     // 到达currentMax,即当前下标i==currentMax
                currentMax = nextMax;   // 进行一次跳跃，currentMax更新为nextMax
                steps++;
            }
        }
        return steps;
    }
}

46. 全排列

LeetCode 46. 全排列

回溯算法

官方题解

根据题意可得出如下草图：

在回溯过程中，我们需要的状态变量有：

  • 递归到了第几层depth（逻辑上即为path中已有的元素个数）
  • 已经选了哪些数path（过程变量）
  • 布尔数组used（存储数组中元素的使用情况）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        int length = nums.length;
        Deque<Integer> path = new ArrayDeque<>();   // 状态变量
        boolean[] used = new boolean[length];  // 状态变量（false表示没有使用，true为已使用）
        dfs(nums,length,0,used,path,result);
        return result;
    }

    private void dfs(int[] nums, int length, int depth, boolean[] used, Deque<Integer> path, List<List<Integer>> result) {
        if (depth==length){     // 递归出口
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < length; i++) {
            if (used[i]){   // 当前数已被使用
                continue;
            }
            // 当前数未被使用
            path.addLast(nums[i]);
            used[i] = true;
            dfs(nums, length, depth+1, used, path, result);
            // 递归结束后别忘了回溯状态变量
            path.removeLast();
            used[i] = false;
        }
    }
}

47. 全排列 II

LeetCode 47. 全排列 II

回溯算法

像这种nums数组中有重复元素的处理，我们选择跟[90. 子集 II](#90. 子集 II)一样，使用Set来处理。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        Set<List<Integer>> result = new HashSet<>();
        int length = nums.length;
        Deque<Integer> path = new ArrayDeque<>();   // 状态变量
        boolean[] used = new boolean[length];  // 状态变量（false表示没有使用，true为已使用）
        dfs(nums,length,0,used,path,result);
        return new ArrayList<>(result) ;
    }

    private void dfs(int[] nums, int length, int depth, boolean[] used, Deque<Integer> path, Set<List<Integer>> result) {
        if (depth==length){     // 递归出口
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < length; i++) {
            if (used[i]){   // 当前数已被使用
                continue;
            }
            // 当前数未被使用
            path.addLast(nums[i]);
            used[i] = true;
            dfs(nums, length, depth+1, used, path, result);
            // 递归结束后别忘了回溯状态变量
            path.removeLast();
            used[i] = false;
        }
    }
}

50. Pow(x, n)

LeetCode 50. Pow(x, n)

分治算法

在看分治法之前，我们先来看一下简单的暴力算法。

最简单的暴力算法，时间复杂度为O(n)。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public double myPow(double x, int n) {
        if (n==0){
            return 1;
        }
        double ans = 1;
        if (n>0){
            for (int i = 0; i < n; i++) {
                ans = ans*x;
            }
        }else {
            for (int i = 0; i < -n; i++) {
                ans = ans*(1/x);
            }
        }
        return ans;
    }
}

结果自然是超时了，Time Limit Exceeded。所以还是需要用分治法来解。

分治法的思想就是拆分若干个子问题，然后将子问题的解结合起来得到题解。

这题我们的分治思想是：将Pow(x,n)分解为pow(x,n/2)这样的子问题，最后根据子问题的解求出题解（这里注意一下奇偶性的不同，合并处理不一样）。

以求2^10为例：

使用分治法就只需要进行4次乘法而不是暴力算法的10次，时间复杂度为O(logN)。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public double myPow(double x, int n) {
        if (n == 0) {
            return 1;
        }
        // 先将n转成正数，后面返回结果时再处理n为负数的情况
        // 注意这里n要为long类型的，不然后面会报java.lang.StackOverflowError
        double ans = divideGenerate(x, Math.abs((long) n));
        if (n>0){
            return ans;
        }else {
            return 1/ans;
        }
    }

    // 分治法
    private double divideGenerate(double x, long n) {
        // 1.终止条件
        if (n==1){
            return x;   // x^1 = x
        }
        // 2.子问题
        double sub = divideGenerate(x, n / 2);
        // 3.合并
        if (n%2==0){
            return sub*sub;
        }else{
            return sub*sub*x;
        }
    }
}

结果为：解答成功:执行耗时:0 ms,击败了100.00% 的Java用户，内存消耗:36.3 MB,击败了94.66% 的Java用户

最开始我写的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public double myPow(double x, int n) {
        if (n==0){
            return 1;
        }
        if (n<0){   // 对n为负数的处理
            n = -n;
            x = 1/x;
        }
        return divideGenerate(x, n);
    }

    // 分治法
    private double divideGenerate(double x, int n) {
        // 1.终止条件
        if (n==1){
            return x;   // x^1 = x
        }
        // 2.子问题
        double sub = divideGenerate(x, n / 2);
        // 3.合并
        if (n%2==0){
            return sub*sub;
        }else{
            return sub*sub*x;
        }
    }
}

但是会报java.lang.StackOverflowError，原因还没分析出来。后来将代码修改成以上代码，就跑通了。

53. 最大子数组和

LeetCode 53. 最大子数组和

贪心算法

这题需要用贪心思想简单分析，就可以得出时间复杂度为O(n)的算法，而不是完全暴力的O(n^2)。

贪心思想：在遍历过程中，如果前面几个数加起来的和temp<0了，那下一个数当然不愿意加上前面的和，所以就舍去前面的子数组，重新开始计算连续子数组和。

我们用max来存储最大值，temp来存储遍历过程中子数组的和。在遍历过程中：

  • 如果temp<0，那么就舍去前面的数，从i开始继续向下遍历（temp=nums[i]）
  • 如果temp>=0，继续向下遍历即可
  • 注意更新max

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int maxSubArray(int[] nums) {
        int temp = nums[0];
        int max = nums[0];
        for (int i = 1; i < nums.length; i++) {
            if (temp<0){
                temp = nums[i];
            }else {
                temp = temp+nums[i];
            }
            max = Math.max(max,temp);
        }
        return max;
    }
}

55.跳跃游戏

LeetCode 55.跳跃游戏

贪心算法

有关动态规划的问题，大多是让你求最值的，比如最长子序列，最小编辑距离，最长公共子串等等等。这就是规律，因为动态规划本身就是运筹学里的一种求最值的算法。

那么贪心算法作为特殊的动态规划也是一样，一般也是让你求个最值。这道题表面上不是求最值，但是可以改一改：请问通过题目中的跳跃规则，最多能跳多远？如果能够越过最后一格，返回 true，否则返回 false。

所以说，这道题肯定可以用动态规划求解的。但是由于它比较简单，这里直接上贪心的思路：

这里，我们用贪心的思想，求出前n-1个数（注意是前n-1个数，因为最后一个数是多少并不重要，只要能到达最后一个数所在的下标即可。n = nums.length）。能到达的下标的最大值farthest是否>=n-1（n-1即为nums最后一个数所在下标）。

前n-1个数在代码中体现在：for (int i = 0; i < n-1; i++)

分析：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public boolean canJump(int[] nums) {
        int farthest = 0;   // 最远距离（所在下标）
        int n = nums.length;
        for (int i = 0; i < n-1; i++) {   // 注意，这里是i<n-1，因为我们要判断的是前n-1个数能到大的最远下标farthest能否到达终点(下标n-1)（特例如：[3,0,0,0]）
            farthest = Math.max(farthest,i+nums[i]);    // 求出能走的最远距离（所在下标）
            if (farthest <= i){  // 如果最大距离（所在下标）都小于或等于i了，说明i之前的数字无论如何也无法跳跃到i之后（中途遇到0卡住了）
                return false;
            }
        }
        return farthest>=n-1;    // 若最远距离恰好是终点，即farthest=n-1，所以判断标准为farthest>=n-1
    }
}

56.合并区间

LeetCode 56.合并区间

暴力算法

分析：先将区间按照指定规则排序。排序规则为：先按照start升序排序，若start一样，则按照end进行升序排序。排序结束后就开始遍历ArrayList了，首先要明确区间合并条件：若start(i)<=start(i+1)<=end(i)，那么就合并第i个和第i+1个区间为新的区间[start(i),Math.max(end(i),end(i+1))]。（注意end值要取两个中的最大值）（这个合并逻辑画一下图就能搞清楚了）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int[][] merge(int[][] intervals) {
        int n = intervals.length;   // 一共n个区间
        ArrayList<int[]> arrayList = new ArrayList<>(n); // 定义ArrayList存储一维数组(区间)
        // 排序二维数组
        Arrays.sort(intervals, new Comparator<int[]>() {
            // 定义排序规则
            @Override
            public int compare(int[] o1, int[] o2) {
                if (o1[0]==o2[0]){  //  start相同，按end升序排序
                    return o1[1]-o2[1];
                }
                return o1[0]-o2[0];
            }
        });
        // 将排序后的intervals全部存入到ArrayList中
        Collections.addAll(arrayList, intervals);
        for (int i = 0; i < arrayList.size()-1; i++) {  // 注意
            // 合并区间条件
            if (arrayList.get(i)[0]<=arrayList.get(i+1)[0]&&
                    arrayList.get(i+1)[0]<=arrayList.get(i)[1]){
                arrayList.set(i, new int[]{arrayList.get(i)[0], Math.max(arrayList.get(i)[1],arrayList.get(i+1)[1])});
                arrayList.remove(i+1);
                i--;    // 合并后要用合并的区间继续跟其他区间比较
            }
        }
        return arrayList.toArray(new int[arrayList.size()][2]);
    }
}

注意：上述代码中我们对二维数组进行了排序，这里给出参考资料：Java Arrays.sort方法重写及二维数组排序，Java Collections工具类（Comparable和Comparator）。

其中排序那段代码还可以用Lambda表达式替换，直接Alt+Enter即可：

1
2
3
4
5
6
7
8
// 定义排序规则，排序二维数组
// 使用Lambda表达式
Arrays.sort(intervals, (o1, o2) -> {
    if (o1[0]==o2[0]){  //  start相同，按end升序排序
        return o1[1]-o2[1];
    }
    return o1[0]-o2[0];
});

毕竟是暴力算法，用时太长了。运行结果为：解答成功:执行耗时:14 ms,击败了6.59% 的Java用户，内存消耗:40.4 MB,击败了97.17% 的Java用户。（本来想用贪心做的，莫名其妙卡进暴力了，难受＞﹏＜）

优化前我新建了区间类继承Comparable接口，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    public int[][] merge(int[][] intervals) {
        int n = intervals.length;   // 一共n个区间
        ArrayList<Interval> arrayList = new ArrayList<>(n);
        for (int[] interval : intervals) {
            arrayList.add(new Interval(interval[0], interval[1]));
        }
        arrayList.sort(Interval::compareTo);    // 按照我们规定的规则将区间排序
        /* 执行合并区间 */
        for (int i = 0; i < arrayList.size()-1; i++) {
            // 合并条件
            if (arrayList.get(i).start<=arrayList.get(i+1).start&&
                    arrayList.get(i+1).start <= arrayList.get(i).end){
                // 注意这里end的新值要取两个中的最大值（从合并区间的条件中可以看出）
                arrayList.set(i,new Interval(arrayList.get(i).start,Math.max(arrayList.get(i).end,arrayList.get(i+1).end)));
                arrayList.remove(i+1);
                i--;    // 合并后要用合并的区间继续跟其他区间比较
            }
        }
        /* arrayList转为二维数组 */
        int[][] result = new int[arrayList.size()][2];
        for (int i = 0; i < arrayList.size(); i++) {
            result[i][0] = arrayList.get(i).start;
            result[i][1] = arrayList.get(i).end;
        }
        return result;
    }

    /**
     * 定义区间类
     */
    public static class Interval implements Comparable<Interval>{
        public int start;
        public int end;

        public Interval(int start, int end) {
            this.start = start;
            this.end = end;
        }

        /**
         * 排序规则：先按照start升序排序，若start一样，按照end升序排序
         * @param o
         * @return
         */
        @Override
        public int compareTo(Interval o) {
            if (this.start==o.start){
                return this.end - o.end;
            }else {
                return this.start - o.start;
            }
        }
    }
}

运行结果为：解答成功:执行耗时:14 ms,击败了6.59% 的Java用户，内存消耗:40.5 MB,击败了95.83% 的Java用户

贪心算法+Stack

该算法题解参考liweiwei1419大佬的贪心题解，这里仅做搬运。

分析：相较于相面的暴力算法，贪心算法只需要我们对start进行升序排序。通过画图我们可以发现，合并条件为：只要有交集的区间就可以合并。在对start进行升序排序后，遍历区间数组（二维数组**，从第二个区间开始跟前一个区间进行对比**），贪心思想如下：

  • 如果遍历的区间的start>结果集中最后一个区间end，说明两个区间没有交集无法合并，直接将遍历的区间push到结果集中
  • 如果遍历的区间的start<=结果集中最后一个区间end，说明两个区间有交集可以合并，这时我们的处理为：修改结果集中的最后一个区间的end，新的end值取遍历的区间end和结果集中最后一个区间end值的最大值（注意这里要去两个中的最大值，画一下图就能理解了）。（start不变因为我们已经对初始区间数组按照start生序排序了）

贪心思想明确了，代码就很明确了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int[][] merge(int[][] intervals) {
        // 结果集我们选择使用Stack，因为只需要对结果集的最后一个元素进行操作(也可以用ArrayList)
        Stack<int[]> result = new Stack<>();
        // 区间集合按照start生序排序（这里用了Lambda表达式）
        Arrays.sort(intervals, (o1, o2) -> o1[0]-o2[0]);
        result.push(intervals[0]);  // 将排序后的第一个区间先push到结果集中
        // 根据贪心思想进行遍历
        for (int i = 0; i < intervals.length; i++) {
            if (intervals[i][0]>result.peek()[1]){  // 遍历的区间的start>结果集中最后一个区间end
                /* 两个区间没有交集无法合并，直接将该区间push到结果集中 */
                result.push(intervals[i]);
            }else { // 遍历的区间的start<=结果集中最后一个区间end,根据我们的分析合并区间
                int newEnd = Math.max(intervals[i][1],result.peek()[1]);
                int[] interval = new int[]{result.peek()[0],newEnd};    // 更新后的区间
                // 更新result，先pop旧的区间，再push新的区间
                result.pop();
                result.push(interval);
            }
        }
        return result.toArray(new int[result.size()][2]);
    }
}

运行结果为：解答成功:执行耗时:8 ms,击败了25.72% 的Java用户，内存消耗:40.7 MB,击败了87.91% 的Java用户。（其实还可以再优化一下，在下面给出了大佬题解的原代码）

复杂度分析：

  • 时间复杂度：O(NlogN)，这里 N 是区间的长度
  • 空间复杂度：O(N)，保存结果集需要的空间，这里计算的是最坏情况，也就是所有的区间都没有交点的时候

说明：Arrays.sort(intervals, (o1, o2) -> o1[0]-o2[0]); 是 Java8 以后提供的一种函数式编程语法。等同于如下代码：

1
2
3
4
5
6
Arrays.sort(intervals, new Comparator<int[]>() {
    @Override
    public int compare(int[] o1, int[] o2) {
        return o1[0]-o2[0];
    }
});

这题在多次提交后的runtime误差好大，而且相同的代码提交之后误差也好大。LeetCode 的 Runtime 指标是否可信？这篇博客中给出了以下总结：

  • 这是玄学
  • 英文版的服务器比中文版的服务器好
  • 尽量挑没人做题的时候提交
  • 以后除非有更好的思路和方法，再也不做优化！

以上代码是我根据大佬题解思路自己敲的。

这里给出大佬题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class Solution {
    public int[][] merge(int[][] intervals) {
        int len = intervals.length;
        if (len < 2) {
            return intervals;
        }
        // 按照起点排序
        Arrays.sort(intervals, Comparator.comparingInt(o -> o[0]));
        // 也可以使用 Stack，因为我们只关心结果集的最后一个区间
        List<int[]> res = new ArrayList<>();
        res.add(intervals[0]);
        for (int i = 1; i < len; i++) {
            int[] curInterval = intervals[i];
            // 每次新遍历到的列表与当前结果集中的最后一个区间的末尾端点进行比较
            int[] peek = res.get(res.size() - 1);
            if (curInterval[0] > peek[1]) {
                res.add(curInterval);
            } else {
                // 注意，这里应该取最大
                peek[1] = Math.max(curInterval[1], peek[1]);
            }
        }
        return res.toArray(new int[res.size()][]);
    }
}

运行结果为：解答成功:执行耗时:7 ms,击败了48.71% 的Java用户，内存消耗:40.8 MB,击败了80.93% 的Java用户

队列（接近双百）

搬运自thiner大佬的题解

上面的暴力算法、贪心算法和官方提供的题解都要先将初始数组进行排序。而如果我们使用队列来处理，就**无需对初始的区间数组进行排序**。这样的结果就接近双百了。

分析：使用队列merged存储答案，在遍历intervals数组时，将merged队列中的元素逐个弹出（结果区间中弹出的区间记为resultInterval），与当前区间currentInterval比较

  • 如果有可以合并区间，则将当前currentInterval区间更新，将更新后的区间add到队列中，并继续与merged队列中的剩余元素比较，直至完成一次队列循环
  • 如果不能合并区间，则将结果集中不能合并区间resultInterval，add到队列中，退出while循环后再将不能和合并的currentInterval区间add到队列中

注意：由于这个算法并没有将初始区间数组进行排序，所以我们的判定是否能合并的条件和合并的规则和上面的贪心算法有所不同：

  • 判断区间是否能合并：我们取min为currentInterval[0]和resultInterval[0]的最小值，max为currentInterval[1]和resultInterval[1]的最大值。如果max-min<=(currentInterval[1]-currentInterval[0])+(resultInterval[1]-resultInterval[0])，就说明可以合并。（画个图就能理解了）
  • 合并规则：合并后的区间为[min,max]（画图就能理解）。在代码中我们可以这样处理：将currentInterval重置为[min,max]，因为在while循环后（结果队列遍历完成后），我们会将currentInterval区间add到队列中的

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int[][] merge(int[][] intervals) {
        /* 用标准库中的LinkedList来模拟队列 */
        Deque<int[]> merged = new LinkedList<>();
        merged.add(intervals[0]);   // 先将数组中的第一个区间插入到队列尾中
        /* 遍历给定的区间数组 */
        for (int i = 1; i < intervals.length; i++) {    // 第一个已经插入到队列了，i可以从1开始
            int k = merged.size();  // 每次遍历数组时队列长度都要重新获取
            int[] currentInterval = intervals[i];
            /* 遍历队列 */
            while (k>0){
                int[] resultInterval = merged.poll();
                int min = Math.min(currentInterval[0],resultInterval[0]);
                int max = Math.max(currentInterval[1],resultInterval[1]);
                // 合并条件
                if (max-min<=(currentInterval[1]-currentInterval[0])+(resultInterval[1]-resultInterval[0])){
                    currentInterval[0] = min;
                    currentInterval[1] = max;
                }else {
                    merged.add(resultInterval); // 不能遍历，让resultIntervala回到队列中（此时add进队尾了）
                }
                k--;
            }
            // 注意：一定要在while循环结束后才将当前interval加入队列，否则可能导致死循环
            merged.add(currentInterval);
        }
        return merged.toArray(new int[merged.size()][2]);
    }
}

时间复杂度：O(nlog(n))，空间复杂度：O(n)。运行结果为：解答成功:执行耗时:2 ms,击败了99.25% 的Java用户，内存消耗:39.9 MB,击败了99.73% 的Java用户

BitSet（无排序，2ms）

该算法是在评论区中参考兰博大佬的。

java BitSet类

大佬题解代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int[][] merge(int[][] intervals) {
        BitSet bitSet = new BitSet();
        int max = 0;
        for (int[] interval : intervals) {
            int temp = interval[1] * 2 + 1;
            bitSet.set(interval[0] * 2, temp, true);
            max = temp >= max ? temp : max;
        }

        int index = 0, count = 0;
        while (index < max) {
            int start = bitSet.nextSetBit(index);
            int end = bitSet.nextClearBit(start);

            int[] item = {start / 2, (end - 1) / 2};
            intervals[count++] = item;

            index = end;
        }
        int[][] ret = new int[count][2];
        for (int i = 0; i < count; i++) {
            ret[i] = intervals[i];
        }

        return ret;
    }
}

结果为：解答成功:执行耗时:2 ms,击败了99.22% 的Java用户，内存消耗:40.9 MB,击败了57.72% 的Java用户

根据提示改进，max可以直接用bitSet.length。改进代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int[][] merge(int[][] intervals) {
        BitSet bitSet = new BitSet();
        for (int[] interval : intervals) {
            bitSet.set(interval[0] * 2, interval[1] * 2 + 1, true);
        }
        int index = 0, count = 0;
        while (index < bitSet.length()) {
            int start = bitSet.nextSetBit(index);
            int end = bitSet.nextClearBit(start);
            int[] item = {start / 2, (end - 1) / 2};
            intervals[count++] = item;
            index = end;
        }
        int[][] ret = new int[count][2];
        for (int i = 0; i < count; i++) {
            ret[i] = intervals[i];
        }
        return ret;
    }
}

位图法我还不是特别熟。大佬的这个题解我大概看明白了，但是让我自己写一个这样的还真不太行…

67. 二进制求和

LeetCode 67. 二进制求和

模拟+栈

在写完[43. 字符串相乘](#43. 字符串相乘)之后，对于将结果存储在数组中的一些思想就很容易想到了。很容易得出结论：两个二进制相加，结果的长度最多为其中最长二进制长度+1。由此我们可以确定最终结果数组的长度。

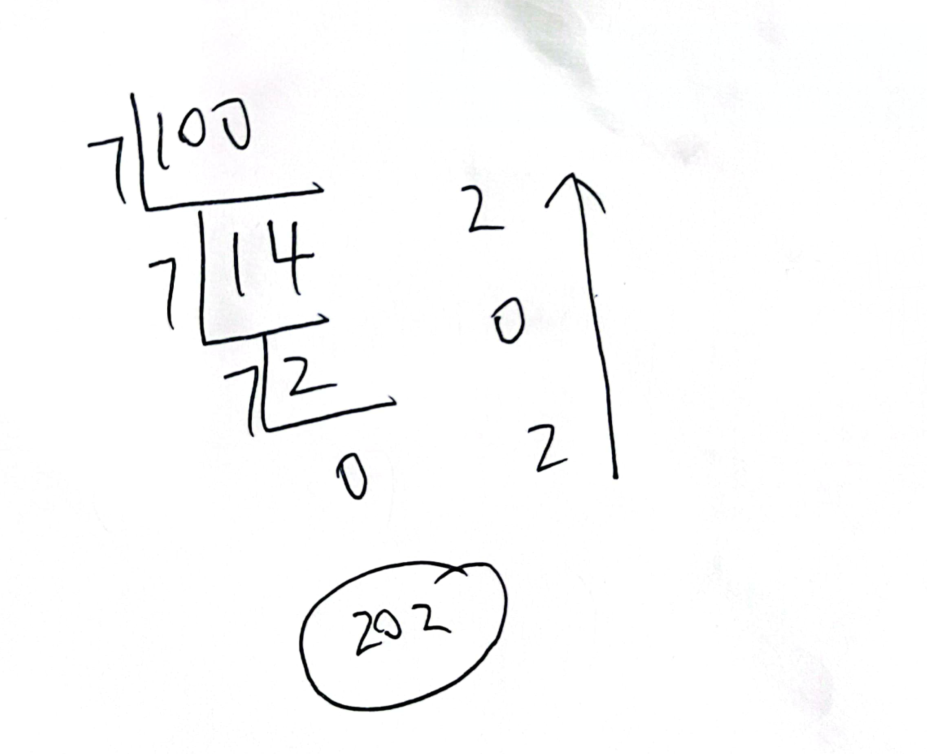
草稿如下：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution {
    public String addBinary(String a, String b) {
        int length_a = a.length();
        int length_b = b.length();
        int length = Math.max(length_a, length_b) + 1;  // 最终结果最大长度
        ArrayDeque<Integer> stack_a = new ArrayDeque<>();
        ArrayDeque<Integer> stack_b = new ArrayDeque<>();
        ArrayDeque<Integer> stack = new ArrayDeque<>(); // 存储最终结果的栈
        for (int i = 0; i < length_a; i++) {
            stack_a.addLast(a.charAt(i)-'0');
        }
        for (int i = 0; i < length_b; i++) {
            stack_b.addLast(b.charAt(i)-'0');
        }
        while (!stack_a.isEmpty() || !stack_b.isEmpty()){
            // 竖式加法，空位补0
            int numa = 0;
            int numb = 0;
            if (!stack_a.isEmpty()){
                numa = stack_a.removeLast();
            }
            if (!stack_b.isEmpty()){
                numb = stack_b.removeLast();
            }
            stack.addLast(numa+numb);
        }
        // 将stack中的数存储到数组中，方便进位处理
        int[] arr = new int[length];
        for (int i = 0; i < length; i++) {
            if (stack.isEmpty()){
                break;
            }
            arr[i] = stack.removeFirst();
        }
        // 进位处理
        for (int i = 0; i < length; i++) {
            if (arr[i]>=2){
                arr[i] = arr[i]%2;
                arr[i+1]++;
            }
        }
        // 对结果首位是否为0的处理
        StringBuilder ans = new StringBuilder();
        if (arr[length-1]!=0){
            ans.append(arr[length-1]);
        }
        for (int i = arr.length - 2; i >= 0; i--) {
            ans.append(arr[i]);
        }
        return ans.toString();
    }
}

69. x 的平方根

LeetCode 69. x 的平方根

二分查找

参考liweiwei1419大佬题解

从题目的要求和示例我们可以看出，这其实是一个查找整数的问题，并且这个整数是有范围的。根据二分查找的思想：

  • 如果这个整数的平方 恰好等于 输入整数x，那么我们就找到了这个整数；
  • 如果这个整数的平方 严格大于 输入整数x，那么这个整数肯定不是我们要找的那个数；
  • 如果这个整数的平方 严格小于 输入整数x，那么这个整数 可能 是我们要找的那个数（举个例子，2*2=4<8，但是8开根号的整数部分正好是2）。

二分查找的关键，是弄清楚mid的取值和搜索区间的更新。一开始我也是经常弄混导致死循环或结果比正确结果多1，最后参考大佬题解后成功AC。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int mySqrt(int x) {
        // 特殊值判断
        if (x==0 || x==1){
            return x;
        }
        int left = 1;
        int right = x/2;    // right取x/2即可
        while (left<right){
            int mid = (left+right+1)/2;
            if (mid>x/mid){     // 用除法防止乘法溢出
                right = mid-1;  // mid肯定不是，更新搜索区间为[left,mid-1]
            }else {
                left = mid;     // mid可能是，更新搜索区间为[mid,right]
            }
        }
        return left;
    }
}

复杂度分析：

  • 时间复杂度：O(logx)。每一次搜索的区间大小约为原来的1/2，时间复杂度为 O(log2x)=O(logx)
  • 空间复杂度：O(1)。

71. 简化路径

LeetCode 71. 简化路径

模拟+栈

来自宫水三叶大佬的题解：【宫水三叶】简单字符串模拟题

根据题意，使用栈进行模拟即可。

具体的，从前往后处理 path，每次以 item 为单位进行处理（有效的文件名），根据 item 为何值进行分情况讨论：

  • item 为有效值 ：存入栈中；
  • item 为 .. ：弹出栈顶元素（若存在）；
  • item 为 . ：不作处理。

举个例子：

至于如何识别有效文件名，只需要用到双指针即可：

  • 指针i在遇到/后，继续向右移动一个单位（i++）
  • 指针i在遇到非/后，此时指针j移动到i的下一位（j=i+1）
  • 此时判断指针j是否遇到/，若遇到了，此时有效文件名item即为path.substring(i, j)；若没有遇到/，指针j继续向右移动（j++）直到遇到为止。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public String simplifyPath(String path) {
        int length = path.length();
        ArrayDeque<String> stack = new ArrayDeque<>();
        // 这个遍历一是想栈中存储有效的文件名item；而是遇到..后pop出栈顶元素
        for (int i = 1; i < length; ) { // path是一个有效的 Unix 风格绝对路径,i=0一定指向/。所以i=1开始
            if (path.charAt(i)=='/'){   // 指针i在遇到/后，继续向右移动一个单位（i++）
                i++;
                continue;
            }
            int j = i+1;    // 指针i在遇到非/后，此时指针j移动到i的下一位（j=i+1）
            while (j<length && path.charAt(j)!='/'){    // 若没有遇到/，指针j继续向右移动（j++）直到遇到为止
                j++;
            }
            // 若j遇到/了，此时有效文件名item即为path.substring(i, j)
            String item = path.substring(i, j);
            if (item.equals("..")){
                if (!stack.isEmpty()){ // 要执行removeLast()操作，肯定要保证stack不为空
                    stack.removeLast();
                }
            }else if (!item.equals(".")){   // 这里的!item.equals(".")就比较灵性了，因为如果是“.”的话我们应该什么也不做
                stack.addLast(item);
            }
            // 最后，i指针指向j指针的下一个位置
            i = j+1;
        }
        // 最终的栈确定下来后，简化后的路径就很好确定了
        StringBuilder ans = new StringBuilder();
        while (!stack.isEmpty()){
            ans.append("/");
            ans.append(stack.removeFirst());    // 注意这里是removeFirst！打下草稿就清楚了
        }
        return ans.length()==0? "/": ans.toString();    // 如果最后栈为空的话，ans应该是/而不是空
    }
}

复杂度分析：

  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

73. 矩阵置零

LeetCode 73. 矩阵置零

二维数组的一维表示

跟以前做过的一样，对于一个行数为 m，列数为 n，行列下标都从 0 开始编号的二维数组，我们可以通过下面的方式，将其中的每个元素 (i, j) 映射到整数域内，并且它们按照行优先的顺序一一对应着 [0, m*n)中的每一个整数。形象化地来说，我们把这个二维数组排扁成了一个一维数组。

这样的映射即为：

(i,j)→i×n+j(i, j) \rightarrow i \times n+j

同样地，我们可以将整数 x 映射回其在矩阵中的下标，即：

{i=x/nj=x%n\left\{\begin{array}{l} i=x / n \\ j=x \% n \end{array}\right.

这个搞清楚了，这题就很好解了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        List<Integer> list = new ArrayList<>();
        for (int x = 0; x <  m * n; x++) { // 记录为0的位置
            if (matrix[x/n][x%n]==0){
                list.add(x);
            }
        }
        for (Integer x : list) {   // 当前行和列需要全置0
            for (int c = 0; c < n; c++) {   // 当前行置0
                matrix[x/n][c] = 0;
            }
            for (int r = 0; r < m; r++) {   // 当前列置0
                matrix[r][x%n] = 0;
            }
        }
    }
}

结果为：执行耗时:1 ms,击败了69.31% 的Java用户，内存消耗:42.9 MB,击败了22.99% 的Java用户

数组

这题就直接嵌套两层for循环，无需什么二维数组的一维化，效率还更高些。

主要思路就是：

  • 只要第i行有0，那么整个第i行都要为0
  • 只要第j列有0，那么整个第j列都要为0

结合代码画个草图就能搞懂了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        boolean[] row = new boolean[m]; // 第i行是否有0
        boolean[] col = new boolean[n]; // 第j列是否有0
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j]==0){   // 第i行，j列有0
                    row[i] = true;
                    col[j] = true;
                }
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (row[i] || col[j]){  // 注意这里是或
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

结果为：解答成功:执行耗时:0 ms,击败了100.00% 的Java用户，内存消耗:42.8 MB,击败了26.63% 的Java用户

78. 子集

LeetCode 78. 子集

回溯算法

liweiwei大佬视频题解。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> result = new ArrayList<>(); // 最终结果
        int length = nums.length;
        // 对数组长度的特殊判断
        if (length==0){
            return result;
        }
        List<Integer> path = new ArrayList<>(); // 记录回溯过程中的结果
        dfs(nums,length,0,path,result);
        return result;
    }

    /**
     *
     * @param nums 题目所给数组
     * @param length 题目所给数组长度，因为不想在dfs函数中每次都去读取nums.length，所以直接将其作为参数
     * @param index 当前遍历到nums数组的索引（当index==length，不能再向下遍历了）
     * @param path 记录回溯过程中的结果
     * @param result 最终返回结果
     */
    private void dfs(int[] nums, int length, int index, List<Integer> path, List<List<Integer>> result) {
        if (index>length-1){ // 不能再向下遍历了，记录结果
            result.add(new ArrayList<>(path));
            return;
        }
        // 在结点的分支中，我们要考虑的是是否要选择当前这个数
        // 1.不选择，直接到下一个结点
        dfs(nums,length,index+1,path,result);

        // 2.选择，将当前这个数添加到path中，然后继续向下一个结点
        path.add(nums[index]);
        dfs(nums,length,index+1,path,result);
        path.remove(path.size()-1); // 别忘了状态变量的还原
    }
}

注意：result.add(new ArrayList<>(path));中，如果只是写成result.add(path);，最后得到的结果全为空[]。

回溯法，还是要子集debug一下才能更详细的体会到。

复杂度分析：

  • 时间复杂度：O(n*2^n)
  • 空间复杂度：O(n*2^n)

82. 删除排序链表中的重复元素II

LeetCode 82. 删除排序链表中的重复元素 II

双指针

这题其实和LeetCode 83. 删除排序链表中的重复元素差不多，只是这里我们需要删除所有重复的元素。最开始，我仿照之前的双指针方法，但是像开头前几个重复元素的情况（如[1,1,1,2,3]）就还是会出问题。后来就突然想到，在链表的题目中我们常用dummyNode来作为链表的头节点，以区分于首元节点。所以我们创建一个dummyNode，其val为-101，保证它不会和链表的其他元素重复，使dummyNode.next = head。

双指针思路如下：定义两个指针p1，p2，初始都指向dummyNode节点。从宏观上看，遍历就是p2指针从dummyNode节点走到链表的最后一个节点。遍历过程中：

  • 首先判断p2节点及以后能否构成连续的3个节点：
    • 若不能，判断p2和p2.next的值：
      • 如果是重复元素，则p2遍历到下一个节点(p2 = p2.next;)，同时p1指向null (p1.next = null;)。说明：因为p2已经遍历到链表的倒数第二个节点了，而p2=p2.next，说明最后两个是重复元素，直接删除即可。
      • 如果不是重复元素，则p2遍历到下一个节点(p2 = p2.next;)，然后p1.next指向p2 (p1.next = p2;)，最后p1也遍历到下一个节点（p1 = p1.next;）。
    • 若能，则判断p2和p2.next还有p2.next.next这三个节点中是否有重复元素：
      • 如果有重复元素，不需要什么额外操作，p2继续遍历到下一个节点(p2 = p2.next;)。
      • 如果没有重复元素，则p2遍历到下一个节点(p2 = p2.next;)，然后p1.next指向p2 (p1.next = p2;)，最后p1也遍历到下一个节点（p1 = p1.next;）。

上面虽然说的复杂，但是逻辑一点也不复杂。简单来说就是判断p2和p2之后的两个节点这三个节点是否有重复元素，如果有，p2遍历到下一个节点；如果没有，p2遍历到下一个节点，然后p1.next指向p2，最后p1也遍历到下一个节点。这个实现逻辑打下草稿就能搞懂。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head==null || head.next==null){
            return head;
        }
        // dummyNode的val设置为-101，保证dummyNode不可能跟链表中任何节点重复
        ListNode dummyNode = new ListNode(-101, head);
        ListNode p1 = dummyNode;
        ListNode p2 = dummyNode;
        // 开始遍历p2
        while (p2.next!=null){  // p2到链表终点，遍历结束
            if (p2.next.next==null){    // p2及之后无法构成3个连续的节点
                if (p2.val!=p2.next.val){
                    p2 = p2.next;
                    p1.next = p2;
                    p1 = p1.next;
                }else {
                    p2 = p2.next;
                    p1.next = null; // 因为p2已经遍历到倒数第二个节点了，而p2=p2.next
                                    // 说明最后两个是重复元素，直接删除即可
                }
            }else {      //  p2及之后可以构成3个连续的节点
                if (p2.val!=p2.next.val && p2.val!=p2.next.next.val
                && p2.next.val!=p2.next.next.val ){ // 连续三个节点都不一样
                    p2 = p2.next;
                    p1.next = p2;
                    p1 = p1.next;
                }else {      // 连续三个节点存在重复
                    p2 = p2.next;
                }
            }
        }
        // 防止链表从开头开始全是重复元素的情况，如[1,1,1]
        if (p1==dummyNode){
            return null;
        }
        return dummyNode.next;
    }
}

官方题解给出的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null) {
            return head;
        }
        ListNode dummy = new ListNode(0, head);
        ListNode cur = dummy;
        while (cur.next != null && cur.next.next != null) {
            if (cur.next.val == cur.next.next.val) {
                int x = cur.next.val;
                while (cur.next != null && cur.next.val == x) {
                    cur.next = cur.next.next;
                }
            } else {
                cur = cur.next;
            }
        }
        return dummy.next;
    }
}

但是我认为，在链表相关的题目中要舍得用变量，如果老是想着节省变量，最后很可能被逻辑绕晕。

评论区中lixiyu大佬的观点，我觉得很对：

  1. 舍得用变量，千万别想着节省变量，否则容易被逻辑绕晕
  2. head 有可能需要改动时，先增加一个假head（dummyNode），返回的时候直接取假dummyNode.next，这样就不需要为修改 head 增加一大堆逻辑了。

83. 删除排序链表中的重复元素

LeetCode 83. 删除排序链表中的重复元素

双指针

因为题目说了链表是已经排序好了的，所以第一次看这题我的想法是：定义两个指针p1，p2，初始都指向头节点，然后移动p2节点开始遍历链表。直到p2走到链表终点。遍历过程中：

  • 遍历开始时，p2先走一步（p2 = p2.next;）
  • 如果p1和p2节点的值不同，那么让p1的下一个节点指向p2（p1.next = p2;），然后让p1走到p2的位置（p1 = p2;）

遍历结束后，因为存在链表的最后几个节点的元素是重复的元素，所以我们还要执行p1.next = null;操作。逻辑很简单，画一下图就能搞懂。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null) {
            return head;
        }
        // p1，p2两个指针，初始都指向head
        ListNode p1 = head;
        ListNode p2 = head;
        while (p2.next != null) {  // p2到链表终点，遍历结束
            p2 = p2.next;
            if (p2.val != p1.val) {   // 发现不同节点
                p1.next = p2;
                p1 = p2;
            }
        }
        // 防止链表的最后几个节点相同的情况
        p1.next = null;
        return head;
    }
}

84. 柱状图中最大的矩形

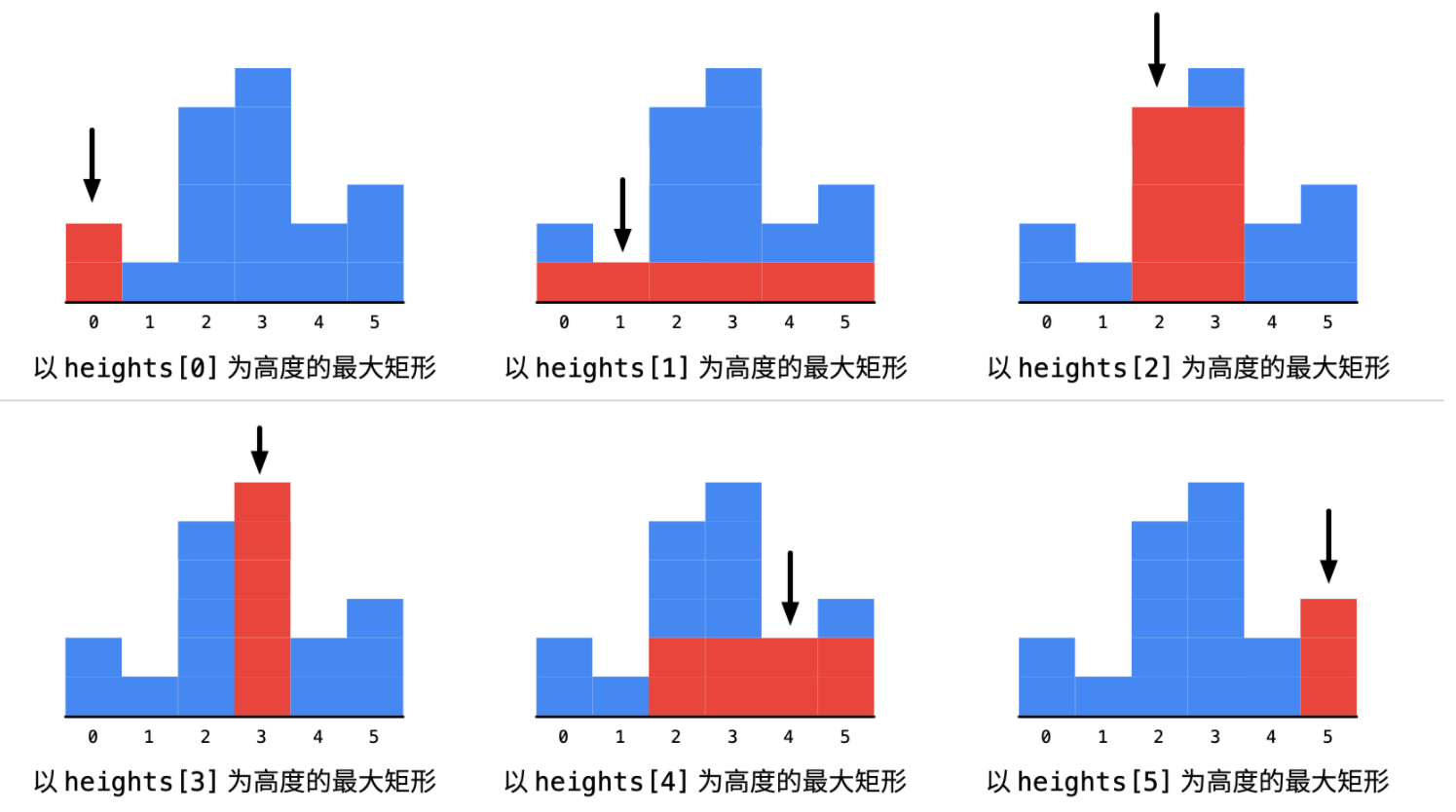
LeetCode 84. 柱状图中最大的矩形

暴力算法（TLE）

暴力算法虽然Time Limit Exceeded，但是写一遍代码，对于理解这题的一些细节上还是很有帮助的。

暴力算法的大致意思是：因为最终的结果一定是一个height*weight的形式，所以我们遍历每一个height，并根据当前的height，向左右扩展来找出最大的weight，最终得到一个max_result。在遍历height时，有一个for循环，在向左右扩展时，会有嵌套的for循环，所以时间复杂度是O(n^2)。

来自liweiwei1419L6大佬的题解分析暴力解法、栈（单调栈、哨兵技巧）

这道问题的暴力解法比「接雨水」那道题要其实好想得多：可以枚举以每个柱形为高度的最大矩形的面积。

具体来说是：依次遍历柱形的高度，对于每一个高度分别向两边扩散，求出以当前高度为矩形的最大宽度多少。

为此，我们需要：

左边看一下，看最多能向左延伸多长，找到大于等于当前柱形高度的最左边元素的下标；
右边看一下，看最多能向右延伸多长；找到大于等于当前柱形高度的最右边元素的下标。
对于每一个位置，我们都这样操作，得到一个矩形面积，求出它们的最大值。

  • 时间复杂度：O(n^2)，这里n是heights数组的长度。
  • 空间复杂度：O(1)，使用常数个临时变量

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int largestRectangleArea(int[] heights) {
        int max_result = 0;
        // 遍历过程中的临时高和宽
        int height = 0;
        int weight = 1;
        for (int i = 0; i < heights.length; i++) {  // 遍历高
            height = heights[i];
            if (height==0){ // 如果该高为0，无需判断weight了
                continue;
            }
            weight = 1;     // weight先置1（即还没向左右遍历的状态，weight为1）
            // 要求遍历过程中的临时宽，需要以i为中心向两边遍历
            for (int l = i - 1; l >= 0; l--) {
                if (heights[l] < heights[i]) { // 如果左边的高比i处的高小，那么就以后都不可以扩展
                        break;
                }
                weight++;
            }
            for (int r = i + 1; r < heights.length; r++) {   // 向右遍历
                if (heights[r] < heights[i]) { // 如果右边的高比i处的高小，那么就以后都不可以扩展
                    break;
                }
                weight++;
            }
            max_result = Math.max(max_result, height * weight);
        }
        return max_result;
    }
}

单调栈

官方题解

这题跟[42. 接雨水](#42. 接雨水)很像，都可以用单调栈来解决。

liweiwei1419大佬的题解已经写得非常详细了，这里写一点自己的想法。

在理解完暴力算法后，就可以很好的理解单调栈的思路了。

使用单调栈解决，在确定某一块不可能再向右扩展后，计算出那一块能确定的最大面积（其实就是能扩展的最大宽度weight，因为height就是这个块）

最后注意一下，我们在单调栈中存储的是各个块在heights数组的索引，这种应该已经遇到过很多次了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
    public int largestRectangleArea(int[] heights) {
        int length = heights.length;
        // 对heights特殊长度的判断
        if (length==0){
            return 0;
        }
        if (length==1){
            return heights[0];
        }

        int max_result = heights[0];    // 初始值
        // 单调栈,如果新push的块让当前栈的栈顶元素不能再扩展了，那么我们就要pop栈顶元素，并计算栈顶那个块能确定的最大面积
        ArrayDeque<Integer> stack = new ArrayDeque<>();
        // for循环遍历数组
        for (int i = 0; i < length; i++) {
            // while循环保证单调栈，同时计算结果
            while (!stack.isEmpty() && heights[i]<heights[stack.peekLast()]){   // 栈顶块不能向右扩展了
                // 求出该pop的块的最大面积
                int curHeight = heights[stack.removeLast()];
                while (!stack.isEmpty() && curHeight==heights[stack.peekLast()]){   // 考虑到新的栈顶元素跟当前块高度一样的情况
                    stack.removeLast();    // 直接pop即可
                }
                int curWeight;  // 接下来要求该块能扩展的最大宽度了
                // 这个特殊情况，一定要画一下草图就能搞懂了
                if (stack.isEmpty()){   // 如果栈顶元素在pop之后为空了，weight为i
                    curWeight = i;
                }else {
                    curWeight = i- stack.peekLast()-1;
                }
                max_result = Math.max(max_result, curHeight*curWeight);
            }
            stack.addLast(i);  // 注意栈中存储的是索引
        }
        // 接下来处理单调栈中剩余的元素
        while (!stack.isEmpty()){
            int curHeight = heights[stack.removeLast()];
            int curWeight;
            // 这个特殊情况，也是要画一下草图就能搞懂了
            if (stack.isEmpty()){   // stack为空了，说明当前pop的栈已经是所有块中最矮的，当然能扩展到尽头
                curWeight = length;
            }else {     // 这个情况画一下图就能搞懂
                curWeight = length-stack.peekLast()-1;
            }
            max_result = Math.max(max_result, curHeight*curWeight);
        }

        return max_result;
    }
}

复杂度分析：

  • 时间复杂度：O(N)，输入数组里的每一个元素入栈一次，出栈一次。
  • 空间复杂度：O(N)，栈的空间最多为 N。

单调栈（哨兵优化）

同样是liweiwei1419大佬的题解。

在上面单纯的使用单调栈时，需要考虑两种特殊的情况：

  1. 弹栈的时候，栈为空
  2. 遍历完成以后，栈中还有元素（所以在for循环之后还有一个while循环处理剩下的单调栈）

为此可以我们可以在输入数组的两端加上两个高度为 0 （或者是 0.5，只要比 1 严格小都行）的柱形，可以回避上面这两种分类讨论。

这两个站在两边的柱形有一个很形象的名词，叫做哨兵（Sentinel）。

有了这两个柱形：

  • 最左边的柱形（第 1 个哨兵）由于它一定比输入数组里任何一个元素小，它肯定不会出栈，因此栈一定不会为空；
  • 最右边的柱形（第 2 个哨兵）也正是因为它一定比输入数组里任何一个元素小，它会让所有输入数组里的元素出栈（第 1 个哨兵元素除外）。

这里栈对应到高度，呈单调增加不减的形态，因此称为单调栈（Monotone Stack）。它是暴力解法的优化，计算每个柱形的高度对应的最大矩形的顺序由出栈顺序决定。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int largestRectangleArea(int[] heights) {
        int length = heights.length;
        // 对heights特殊长度的判断
        if (length==0){
            return 0;
        }
        if (length==1){
            return heights[0];
        }

        int max_result = heights[0];    // 初始值
        // 创建新数组newHeights，与heights相比只是在其两端上各加1个0
        int[] newHeights = new int[length+2];
        newHeights[0] = 0;
        newHeights[length+1] = 0;
        System.arraycopy(heights, 0, newHeights, 1, heights.length);
        length = length+2;  // 此时将length设置为newHeights数组的长度
        // 单调栈
        ArrayDeque<Integer> stack = new ArrayDeque<>();
        stack.addLast(0);   // 添加最左边的哨兵，这样在对单调栈的操作中栈永远不会为空
        for (int i = 1; i < length; i++) {  // 已经添加最左边的哨兵了，所以注意i从1开始
            while (newHeights[i]<newHeights[stack.peekLast()]){
                int curHeight = newHeights[stack.removeLast()];
                int curWeight = i-stack.peekLast()-1;
                max_result = Math.max(max_result,curHeight*curWeight);
            }
            stack.addLast(i);
        }
        return max_result;
    }
}

相比上面的代码，使用哨兵优化代码无疑要简化的多。

88. 合并两个有序数组

LeetCode 88. 合并两个有序数组

排序

先将nums2的数组添加到nums1中，然后对nums1进行排序即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = m;
        int j = 0;
        while (j<n){
            nums1[i] = nums2[j];
            i++;
            j++;
        }
        Arrays.sort(nums1);
    }
}

双指针

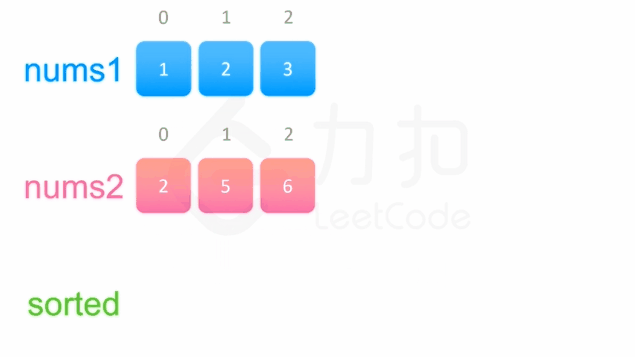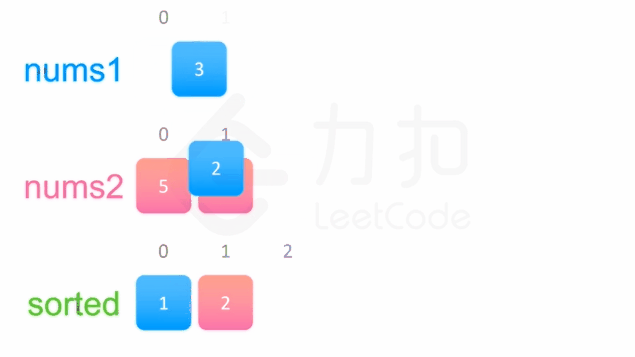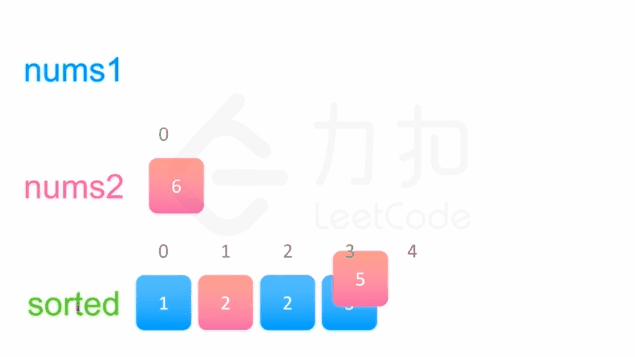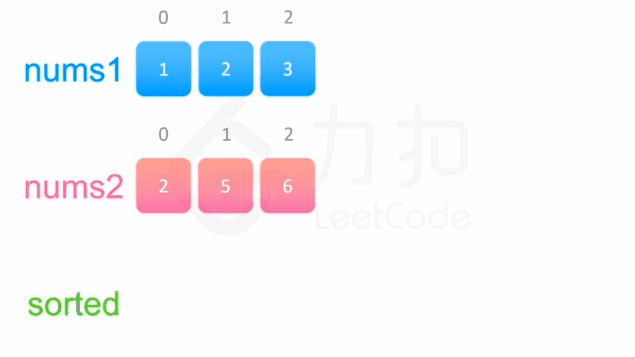
官方题解

思路：定义两个指针分别遍历nums1和nums2。然后按降序将结果存储到新的数组sorted中。最后将nums1变为sorted即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        ArrayList<Integer> sorted = new ArrayList<>();
        // 双指针
        int i = 0;
        int j = 0;
        while (i<m || j<n){
            if (i>=m){  // i指针已经走完nums1了
                sorted.add(nums2[j]);
                j++;
            }else if (j>=n){  // j指针已经走完nums2了（i还没有走完）
                sorted.add(nums1[i]);
                i++;
            }else if (nums1[i]<nums2[j]){   // 都没有走完
                sorted.add(nums1[i]);
                i++;
            }else if (nums2[j]<=nums1[i]){
                sorted.add(nums2[j]);
                j++;
            }
        }
        for (int index = 0; index < sorted.size(); index++) {
            nums1[index] = sorted.get(index);
        }
    }
}

复杂度分析：

  • 时间复杂度：O(m+n)。
  • 空间复杂度：O(m+n)。

逆向双指针

官方题解

方法二中，之所以要使用临时变量，是因为如果直接合并到数组nums1中，nums1中的元素可能会在取出之前被覆盖。那么如何直接避免覆盖 nums1 中的元素呢？观察可知，nums1的后半部分是空的，可以直接覆盖而不会影响结果。因此可以设置指针为从后向前遍历，每次取两者之中的较大者放进nums1的最后面。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        // 逆向双指针
        int i = m-1;
        int j = n-1;
        int end = m+n-1;
        while (end>=0){
            if (i<0){   // i指针走完了
                nums1[end] = nums2[j];
                end--;
                j--;
            }else if (j<0){   // j指针已经走完nums2了（i还没有走完）
                nums1[end] = nums1[i];
                end--;
                i--;
            }else if (nums1[i]>nums2[j]){   // 都没有走完
                nums1[end] = nums1[i];
                end--;
                i--;
            }else {
                nums1[end] = nums2[j];
                end--;
                j--;
            }
        }
    }
}

复杂度分析：

  • 时间复杂度：O(m+n)。
  • 空间复杂度：O(1)。

90. 子集 II

LeetCode 90. 子集 II

回溯算法

这题跟[78. 子集](#78. 子集)很像，只是需要去除重复的子集即可。这里我们使用Set来进行去重。

首先要对nums进行排序。这样是为了后续可以更好地进行去重。大致思路如下：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Set<List<Integer>> result = new HashSet<>(); // 最终结果
        int length = nums.length;
        // 对数组长度的特殊判断
        if (length==0){
            return new ArrayList<>();
        }
        List<Integer> path = new ArrayList<>(); // 记录回溯过程中的结果
        Arrays.sort(nums);
        dfs(nums,length,0,path,result);
        return new ArrayList<>(result);
    }

    /**
     *
     * @param nums 题目所给数组
     * @param length 题目所给数组长度，因为不想在dfs函数中每次都去读取nums.length，所以直接将其作为参数
     * @param index 当前遍历到nums数组的索引（当index==length，不能再向下遍历了）
     * @param path 记录回溯过程中的结果
     * @param result 最终返回结果
     */
    private void dfs(int[] nums, int length, int index, List<Integer> path, Set<List<Integer>> result) {
        if (index>length-1){ // 不能再向下遍历了，记录结果
            result.add(new ArrayList<>(path));
            return;
        }
        // 在结点的分支中，我们要考虑的是是否要选择当前这个数
        // 1.不选择，直接到下一个结点
        dfs(nums,length,index+1,path,result);

        // 2.选择，将当前这个数添加到path中，然后继续向下一个结点
        path.add(nums[index]);
        dfs(nums,length,index+1,path,result);
        path.remove(path.size()-1); // 别忘了状态变量的还原
    }
}

92. 反转链表 II

LeetCode 92. 反转链表 II

单链表（先切割再合并）

官方题解给出的第一种方法，跟我一开始的想法是一样的：即先将要反转的链表片段切割出来，然后执行[206反转链表](#206. 反转链表)的操作，最后将反转后的链表与原链表两端对接即可。这里注意一下，为了处理left的多种情况，我选择使用了头结点root用以区分首元结点head。在写单链表的1一些题目时，有时并不是特别区分头结点和首元结点的叫法。但是我们心里一定要清楚头结点和首元结点。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        if (left == right) {  // left==right,直接返回head即可
            return head;
        }
        // 为了方便起见，我们还是要来用一个头结点root，区别于首元结点head
        ListNode root = new ListNode();
        root.next = head;
        // 反转中间链表，需要重点关注4个结点
        ListNode left_Node = root;  //  left节点的前一个节点
        ListNode leftNode = root;   // left节点
        ListNode rightNode = root;  // right节点
        ListNode rightNode1 = root; // right节点的下一个节点
        for (int i = 0; i < left - 1; i++) {
            left_Node = left_Node.next;
        }
        leftNode = left_Node.next;
        for (int i = 0; i < right; i++) {
            rightNode = rightNode.next;
        }
        rightNode1 = rightNode.next;
        // 切割链表
        left_Node.next = null;
        rightNode.next = null;
        // 反转切割出来的链表,用left-1节点指向反转后的链表的头节点
        left_Node.next = reverseLinkedList(leftNode);
        leftNode.next = rightNode1;     // 反转后的链表，leftNode节点即为最后一个节点
        return root.next;
    }

    private ListNode reverseLinkedList(ListNode head) {
        ListNode pre = null;
        ListNode cur = head;
        while (cur != null) {
            ListNode next = cur.next;
            cur.next = pre; // 修改结点指向
            pre = cur;
            cur = next;
        }
        return pre;
    }
}

头插法

官方题解中给出的第二个方法，即为头插法。这里搬运一下官方题解思路：

方法一的缺点是：如果 left 和 right 的区域很大，恰好是链表的头节点和尾节点时，找到 left 和 right 需要遍历一次，反转它们之间的链表还需要遍历一次，虽然总的时间复杂度为 O(N)O(N)，但遍历了链表 22 次，可不可以只遍历一次呢？答案是可以的。我们依然画图进行说明。

我们依然以方法一的示例为例进行说明。

整体思想是：在需要反转的区间里，每遍历到一个节点，让这个新节点来到反转部分的起始位置。下面的图展示了整个流程。

下面我们具体解释如何实现。使用三个指针变量 pre、curr、next 来记录反转的过程中需要的变量，它们的意义如下：

  • curr：指向待反转区域的第一个节点 left；
  • next：永远指向 curr 的下一个节点，循环过程中，curr 变化以后 next 会变化；
  • pre：永远指向待反转区域的第一个节点 left 的前一个节点，在循环过程中不变。

第 1 步，我们使用 ①、②、③ 标注「穿针引线」的步骤。

操作步骤：

  • 先将 curr 的下一个节点记录为 next；
  • 执行操作 ①：把 curr 的下一个节点指向 next 的下一个节点；
  • 执行操作 ②：把 next 的下一个节点指向 pre 的下一个节点；
  • 执行操作 ③：把 pre 的下一个节点指向 next。

这个循环执行right-left次。

第 1 步完成以后「拉直」的效果如下：

第 2 步，同理。同样需要注意 「穿针引线」操作的先后顺序。

第 2 步完成以后「拉直」的效果如下：

第三步同理，一共执行right-left次后就完成了。

因为代码是我根据头插法的思路自己敲的，所以代码跟官方题解有些不一致，这里说明一下：

  • cur：永远指向 left节点；（在循环的过程中，left-1节点的下一个节点不一定是left（cur）节点了）
  • next：永远指向 cur 的下一个节点，循环过程中，cur 变化以后 next 会变化；
  • left_Node：永远指向待反转区域的第一个节点 left 的前一个节点，在循环过程中不变。

for循环内的**操作步骤**：

  • next节点赋值为 cur 的下一个节点记录为 ；
  • 把 cur 的下一个节点指向 next 的下一个节点；
  • 把 next 的下一个节点指向 left_Node 的下一个节点；
  • 把 left_Node 的下一个节点指向 next。

这个循环执行right-left次。

只看文字可能有点绕，画个草稿应该可以搞清楚。这里可以看一下比较潦草的草稿：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        if (left == right) {  // left==right,直接返回head即可
            return head;
        }
        // 为了方便起见，我们还是要来用一个头结点root，区别于首元结点head
        ListNode root = new ListNode();
        root.next = head;
        // 反转中间链表，需要重点关注4个结点
        ListNode left_Node = root;  //  left节点的前一个节点
        ListNode cur = root;   // left节点
        for (int i = 0; i < left - 1; i++) {
            left_Node = left_Node.next;
        }
        cur = left_Node.next;
        ListNode next;
        // 循环right - left次
        for (int i = 0; i < right - left; i++) {
            next = cur.next;
            cur.next = next.next;
            next.next = left_Node.next;
            left_Node.next = next;
        }
        return root.next;
    }
}

栈

由大佬耗子扛刀一路找猫提供的思路。这种思路并没有像上面两种方法那样对节点的指向(next)进行修改，而是修改链表本身的val值。

分析如下：

  • 要反转链表，只需要将该链表的对称两端节点的val值互换即可
  • 要实现对称互换的效果，可以将要反转的链表分为[left,（left+right）/2+1]，[（left+right）/2+1,right]这两部分，保证这两部分关于链表中心对称
  • 互换的实现可以借助栈，用栈来存储右半部分的节点。

大致思想如下：

大佬代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        ListNode leftNode = head;
        ListNode rightNode = head;
        Stack<ListNode> stack = new Stack<>();
        for(int i = 0; i < (left + right) / 2; i++)
            rightNode = rightNode.next;
        for(int i = (left + right) / 2 + 1; i <= right; i++)
        {
            stack.push(rightNode);
            rightNode = rightNode.next;
        }
        for(int i = 0; i < left - 1; i++)
            leftNode = leftNode.next;
        while(!stack.isEmpty())
        {
            rightNode = stack.pop();
            int temp = rightNode.val;
            rightNode.val = leftNode.val;
            leftNode.val = temp;
            leftNode = leftNode.next;
        }
        return head;
    }
}

94. 二叉树的中序遍历

LeetCode 94. 二叉树的中序遍历

深度优先搜索（DFS）

二叉树的四种遍历在数据结构的学习中就已经实现过了（笔记链接），这里直接给出代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    List<Integer> list = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        if (root!=null){
            inorderTraversal(root.left);
            list.add(root.val);
            inorderTraversal(root.right);
        }
        return list;
    }
}

101. 对称二叉树

LeetCode 101. 对称二叉树

递归

官方题解

如果一个树的左子树与右子树镜像对称，那么这个树是对称的。

判断两个树是否互为镜像：

  • 它们的两个根结点具有相同的值
  • 每个树的右子树都与另一个树的左子树镜像对称

我们可以实现这样一个递归函数，通过同步移动两个指针的方法来遍历这棵树，p 指针和 q 指针一开始都指向这棵树的根，随后 p 右移时，q 左移，p 左移时，q 右移。

每次检查当前 p 和 q 节点的值是否相等，如果相等再判断左右子树是否对称。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root,root);

    }

    private boolean check(TreeNode p, TreeNode q) {
        // 递归出口
        if (p==null && q==null){    // 当p和q都到空了还没用返回false，说明是对称的
            return true;
        }else if (p==null || q==null){  // 出现p为空q不为空或q为空p不为空，不可能是对称的了
            return false;
        }
        // 没有走到递归出口，就递归的判断p和q的值是否相等，p的左子树是否和q的右子树对称，p的右子树是否和q的左子树相等
        return p.val==q.val && check(p.left,q.right) && check(p.right,q.left);
    }
}

复杂度分析：

  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

（n为树的结点数）

102. 二叉树的层序遍历

LeetCode 102. 二叉树的层序遍历

广度优先搜索（BFS）

二叉树的四种遍历在数据结构的学习中就已经实现过了（笔记链接）

但是这里的输出是以嵌套列表的形式输出，所以按照笔记上的那种解法还不够，需要两层while循环来控制每一层在同一个列表中。但是还是用队列来实现，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    List<List<Integer>> lists = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        if (root==null){    // 如果树为空，直接返回空列表
            return lists;
        }
        ArrayDeque<TreeNode> deque = new ArrayDeque<>();    // 用队列来实现
        deque.add(root);
        while (!deque.isEmpty()){
            int count = deque.size();    // 记录队列当前长度，即为当前层的结点数
            List<Integer> list = new ArrayList<>(); // 存储当前层结果列表
            while (count>0){    // 这里是count>0而不是!deque.isEmpty()，就是为了控制每一层的结点在同一个列表中
                TreeNode node = deque.remove();
                list.add(node.val);
                if (node.left!=null){
                    deque.add(node.left);
                }
                if (node.right!=null){
                    deque.add(node.right);
                }
                count--;
            }
            // 上面的while循环结束后，该层的遍历结束
            lists.add(list);
            // 但是由于有deque.add(node.left)和deque.add(node.right)这样的操作
            // count=0只是该层遍历结束，deque还不为空，会继续循环
        }
        return lists;
    }
}

104. 二叉树的最大深度

LeetCode 104. 二叉树的最大深度

深度优先搜索（DFS）

官方题解

使用深度优先搜索的思想。递归地求出二叉树左子树和右子树的深度leftDepth和rightDepth，最后返回Math.max(leftDepth,rightDepth)+1即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
class Solution {
    public int maxDepth(TreeNode root) {
        if (root==null){
            return 0;
        }
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return Math.max(leftDepth,rightDepth)+1;
    }
}

105. 从前序与中序遍历序列构造二叉树

LeetCode 105. 从前序与中序遍历序列构造二叉树

118. 杨辉三角

LeetCode 118. 杨辉三角

数学

根据杨辉三角的概念，嵌套两层for循环求解。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> path;
        for (int i = 0; i < numRows; i++) {
            path = new ArrayList<>();
            for (int j = 0; j <= i; j++) {
                if (j==0 || j==i){
                    path.add(1);
                }else {
                    path.add(res.get(i-1).get(j-1)+res.get(i-1).get(j));
                }
            }
            res.add(path);
        }
        return res;
    }
}

119. 杨辉三角 II

LeetCode 119. 杨辉三角 II

数学

按照LeetCode 118. 杨辉三角中的题解，求出杨辉三角前rowIndex+1行，最后第rowIndex行即为res.get(rowIndex)。（因为题目说从第0行开始算）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> path;
        for (int i = 0; i <= rowIndex; i++) {
            path = new ArrayList<>();
            for (int j = 0; j <= i; j++) {
                if (j==0 || j==i){
                    path.add(1);
                }else {
                    path.add(res.get(i-1).get(j-1)+res.get(i-1).get(j));
                }
            }
            res.add(path);
        }
        return res.get(rowIndex);
    }
}

数学优化

官方题解

因为题目要求第rowIndex的杨辉三角，所以就不需要生成整个杨辉三角。

由组合数公式 Cnm=n!m!(n−m)!\mathcal{C}_{n}^{m}=\frac{n !}{m !(n-m) !} ，可以得到同一行的相邻组合数的关系

Cnm=Cnm−1×n−m+1m\mathcal{C}_{n}^{m}=\mathcal{C}_{n}^{m-1} \times \frac{n-m+1}{m}

由于 Cn0=1\mathcal{C}_{n}^{0}=1 ，利用上述公式我们可以在线性时间计算出第 nn 行的所有组合数。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> res = new ArrayList<>();
        for (int i = 0; i <= rowIndex; i++) {
            if (i==0 || i==rowIndex){
                res.add(1);
            }else { // 注意这里有溢出的问题
                res.add((int) ((long)res.get(i-1) * (rowIndex-i+1)/i));
            }
        }
        return res;
    }
}

121. 买卖股票的最佳时机

LeetCode 121. 买卖股票的最佳时机

单调栈

这题看到之后，首先想到的就是使用单调栈，保证栈顶永远大于栈底。

具体思路用文字不好说，草稿图如下：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int maxProfit(int[] prices) {
        int res = 0;
        ArrayDeque<Integer> stack = new ArrayDeque<>();
        for (int i = 0; i < prices.length; i++) {
            while (!stack.isEmpty() && prices[i]<stack.peekLast()){
                Integer removeLast = stack.removeLast();
                if (!stack.isEmpty()){
                    res = Math.max(res, removeLast-stack.peekFirst());
                }
            }
            stack.addLast(prices[i]);
        }
        // 循环结束后，如果单调栈不为空，别忘了记录此时栈顶-栈底的值
        if (!stack.isEmpty()){
            res = Math.max(res, stack.peekLast()-stack.peekFirst());
        }
        return res;
    }
}

134. 加油站

LeetCode 134. 加油站

贪心算法

分析：主要有两点：

  • 首先，gas数组之和减去cost数组之和sum一定要大于等于0，否则无论如何也不可能绕一圈
  • 在确保可以绕一圈后，就要开始贪心思想了：如果从加油站i到加油站j时，汽车油量oil变成了负数。说明加油站i到加油站j中的任何一个加油站都不可能作为起点。并且加油站j的gas一定小于cost，因此加油站j自己也不可能作为起点。（这里的贪心思想非常关键，通过此思路就可以实现贪心算法而不是暴力算法）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int length = gas.length;
        int[] arr = new int[length];
        for (int i = 0; i < length; i++) {
            arr[i] = gas[i] - cost[i];
        }
        int sum = 0;
        for (int i = 0; i < length; i++) {
            sum = sum+arr[i];
        }
        if (sum<0){     // 不可能绕一圈
            return -1;
        }else {
            int result = 0;
            int oil = 0;    // 剩余油量
            for (int i = 0; i < length; i++) {
                oil = oil+arr[i];
                if (oil<0){     /* 举个例子，若i=0，i=1时，oil都大于0，i=2时oil<0
                                    根据我们分析的贪心算法，这就说明从0到2之间
                                    任意一个加油站都不可能成为起点，result直接取i+1
                                    再重置oil为0 */
                    oil = 0;
                    result = i+1;
                }
            }
            if (result==length){    // 因为是环形，起点为数组长度length，即为起点
                return 0;
            }else {
                return result;
            }
        }
    }
}

136. 只出现一次的数字

LeetCode 136. 只出现一次的数字

位运算

如果要求：算法具有线性时间复杂度，不使用额外空间来实现。那么就不能使用哈希表了。我们可以使用位运算来实现。

由于题目所给的非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。

同时结合简单的数学知识：

  • 相同的数异或运算结果为0
  • 0和任何数进行异或运算都等于这个数本身

所以我们将nums数组中所有数进行异或操作，由于相同的两个数异或结果为0，最终结果即为0异或只出现一次的数字，结果即为这个数字本身。

代码如下：

1
2
3
4
5
6
7
8
9
class Solution {
    public int singleNumber(int[] nums) {
        int result = 0;
        for (int num : nums) {
            result  =result^num;
        }
        return result;
    }
}

141. 环形链表

LeetCode 141. 环形链表

哈希表

思路也比较简单。遍历单链表，使用HashSet来记录遍历过的节点Node。如果出现遍历到的节点的下一个节点node.next在HashSet中出现过，那么就说明是环形链表。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Solution {
    public boolean hasCycle(ListNode head) {
        Set<ListNode> set = new HashSet<>();
        ListNode p = head;
        while (p!=null){
            if (set.add(p.next)){
                p = p.next;
            }else { // 是环形链表
                return true;
            }
        }
        return false;
    }
}

结果为：解答成功:执行耗时:3 ms,击败了22.34% 的Java用户，内存消耗:42 MB,击败了60.67% 的Java用户

快慢指针

在一般面试时，比较经典的回答还是双指针。思路就是：使用两个指针p1，p2。p1指针每次走一步，p2指针每次走两步。在指针走到尽头之前，如果p1等于p2了，那么就说明有环。（事实上如果有环了话，两个指针就永远不刽走到尽头，迟早会相遇的）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head==null){
            return false;
        }
        ListNode p1 = head;
        ListNode p2 = head.next;
        while (p2!=null && p2.next!=null){
            if (p1==p2){
                return true;
            }
            p1 = p1.next;
            p2 = p2.next.next;
        }
        return false;
    }
}

结果为：解答成功:执行耗时:0 ms,击败了100.00% 的Java用户，内存消耗:42.6 MB,击败了24.28% 的Java用户

142. 环形链表 II

LeetCode 142. 环形链表 II

哈希表

使用哈希表思路跟LeetCode 141. 环形链表一样简单，使用HashSet即可解决。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head==null){
            return null;
        }
        HashSet<ListNode> set = new HashSet<>();
        while (head!=null){
            if (set.contains(head)){
                return head;
            }
            set.add(head);
            head = head.next;
        }
        return null;
    }
}

结果为：解答成功:执行耗时:3 ms,击败了20.26% 的Java用户，内存消耗:42.4 MB,击败了5.06% 的Java用户

快慢指针

官方题解

快慢指针，当slow指针和fast指针相遇后，再让ptr指针从头结点开始，和slow指针每次向后移动一个位置。最终，它们会在入环点相遇。

数学推论：

我们使用两个指针，fast 与 slow。它们起始都位于链表的头部。随后， slow指针每次向后移动 一个位置，而 fast 指针向后移动两个位置。如果链表中存在环，则 fast 指针最终将再次与 slow 指针在环中相遇。
如下图所示，设链表中环外部分的长度为 aa 。 slow 指针进入环后，又走了 bb 的距离与 fast 相 遇。此时，fast 指针已经走完了环的 nn 圈，因此它走过的总距离为 a+n(b+c)+b=a+(n+a+n(b+c)+b=a+(n+ 1) b+nc。 b+n c_{\text {。 }}。

根据题意，任意时刻，fast 指针走过的距离都为 slow 指针的 2 倍。因此，我们有

a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)a+(n+1) b+n c=2(a+b) \Longrightarrow a=c+(n-1)(b+c)

有了 a=c+(n−1)(b+c)a=c+(n-1)(b+c) 的等量关系，我们会发现：从相遇点到入环点的距离加上 n−1n-1 圈 的环长，恰好等于从链表头部到入环点的距离。
因此，当发现 slow 与 fast 相遇时，我们再额外使用一个指针 ptr。起始，它指向链表头部；随 后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head==null){
            return null;
        }
        ListNode slow = head;
        ListNode fast = head;
        ListNode ptr = head;
        while (fast!=null && fast.next!=null){
            slow = slow.next;
            fast = fast.next.next;
            if (slow==fast){
                while (ptr!=slow){
                    ptr = ptr.next;
                    slow = slow.next;
                }
                return ptr;
            }
        }
        return null;
    }
}

结果为：解答成功:执行耗时:0 ms,击败了100.00% 的Java用户，内存消耗:41.6 MB,击败了44.39% 的Java用户

144. 二叉树的前序遍历

LeetCode 144. 二叉树的前序遍历

深度优先搜索（DFS）

二叉树的四种遍历在数据结构的学习中就已经实现过了（笔记链接），这里直接给出代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    List<Integer> list = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        if (root!=null){
            list.add(root.val);
            preorderTraversal(root.left);
            preorderTraversal(root.right);
        }
        return list;
    }
}

145. 二叉树的后序遍历

LeetCode 145. 二叉树的后序遍历

深度优先搜索（DFS）

二叉树的四种遍历在数据结构的学习中就已经实现过了（笔记链接），这里直接给出代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    List<Integer> list = new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) {
        if (root!=null){
            postorderTraversal(root.left);
            postorderTraversal(root.right);
            list.add(root.val);
        }
        return list;
    }
}

146. LRU 缓存

LeetCode 146. LRU 缓存

哈希表 + 双向链表

官方题解

LRU 缓存机制可以通过哈希表辅以双向链表实现，我们用一个哈希表和一个双向链表维护所有在缓存中的键值对。

  • 双向链表按照被使用的顺序存储了这些键值对，靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的。
  • 哈希表即为普通的哈希映射（HashMap），通过缓存数据的键映射到其在双向链表中的位置。

这样以来，我们首先使用哈希表进行定位，找出缓存项在双向链表中的位置，随后将其移动到双向链表的头部，即可在 O(1) 的时间内完成 get 或者 put 操作。具体的方法如下：

  • 对于 get 操作，首先判断 key 是否存在：
    • 如果 key 不存在，则返回 −1；
    • 如果 key 存在，则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置，并将其移动到双向链表的头部，最后返回该节点的值。
  • 对于 put 操作，首先判断 key 是否存在：
    • 如果 key 不存在，使用 key 和 value 创建一个新的节点，**在双向链表的头部添加该节点，并将 key 和该节点添加进哈希表中。**然后判断双向链表的节点数是否超出容量，如果超出容量，则删除双向链表的尾部节点，并删除哈希表中对应的项；
    • 如果 key 存在，则与 get 操作类似，先通过哈希表定位，再将对应的节点的值更新为 value，并将该节点移到双向链表的头部。

上述各项操作中，访问哈希表的时间复杂度为 O(1)，在双向链表的头部添加节点、在双向链表的尾部删除节点的复杂度也为 O(1)。而将一个节点移到双向链表的头部，可以分成删除该节点和在双向链表的头部添加节点两步操作，都可以在 O(1) 时间内完成。

在双向链表的实现中，使用一个伪头部（dummy head）和伪尾部（dummy tail）标记界限，这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
class LRUCache {
    // 双向节点类
    class LinkedNode{
        int key;
        int value;
        LinkedNode pre;
        LinkedNode next;

        public LinkedNode() {
        }

        public LinkedNode(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }

    // 定义LRU相关的全局变量
    // key存储key建值，value存储双向节点（包含key和value）
    private Map<Integer, LinkedNode> cache = new HashMap<Integer, LinkedNode>();
    private int size;   // LRUCache大小
    private int capacity;   // 最大容量
    // 伪头结点和末尾结点
    private LinkedNode dummyHead;
    private LinkedNode dummyTail;

    /**
     * 初始化LRUCache
     * @param capacity
     */
    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        dummyHead = new LinkedNode();
        dummyTail = new LinkedNode();
        // 双向链表，互相指向
        dummyHead.next = dummyTail;
        dummyTail.pre = dummyHead;
    }
    
    public int get(int key) {
        LinkedNode linkedNode = cache.get(key);
        if (linkedNode==null){  // key不存在，返回-1
            return -1;
        }
        // key存在，先将该节点移到头部（最近使用），然后返回该节点值
        moveToHead(linkedNode);
        return linkedNode.value;
    }

    public void put(int key, int value) {
        LinkedNode linkedNode = cache.get(key);
        if (linkedNode==null){  // key不存在，需要创建一个新的节点
            LinkedNode newLinkedNode = new LinkedNode(key, value);
            addToHead(newLinkedNode);   // 添加至双向链表的头部
            cache.put(key,newLinkedNode);   // 添加进哈希表
            // 然后要判断容量
            size++;
            if (size>capacity){ // 超出容量
                // 删除双向链表的尾部节点
                LinkedNode tail = removeTail();
                // 删除哈希表中对应的项
                cache.remove(tail.key);
                size--; // 别忘了size--
            }
        }else {     // key存在（linkedNode不为null），更新即可
            linkedNode.value = value;   // 更新节点值
            moveToHead(linkedNode);      //将该节点移到双向链表的头部
        }
    }


    /**
     * 移动指定节点到头部（最近使用）
     * @param linkedNode
     */
    private void moveToHead(LinkedNode linkedNode) {
        // 先删除再插入来实现
        removeNode(linkedNode);
        addToHead(linkedNode);
    }

    /**
     * 添加指定节点到头部
     * @param addNode
     */
    private void addToHead(LinkedNode addNode) {
        // 实现画一下草图就能搞懂
        dummyHead.next.pre = addNode;    // 切断了dummyHead与node节点的pre连接
        addNode.next = dummyHead.next;   // 更新了addNode与node的next连接
        dummyHead.next = addNode;
        addNode.pre = dummyHead;
    }

    /**
     * 删除指定的节点
     * @param removeNode
     */
    private void removeNode(LinkedNode removeNode) {
        removeNode.pre.next = removeNode.next;
        removeNode.next.pre = removeNode.pre;
    }

    /**
     * 删除最后一个节点（最久未使用），并返回
     * @return
     */
    private LinkedNode removeTail() {
        LinkedNode res = dummyTail.pre;
        removeNode(res);    // 删除节点
        return res;         // 返回该节点
    }
}

155. 最小栈

LeetCode 155. 最小栈

栈+辅助栈

官方提供的题解，比我最开始自己写的辅助栈要好多了。

常规解法，一个栈stack来实现push、pop和top操作，另一个辅助栈min_stack用来实现getMin。大体思路是：

  • 每次push的时候，stack正常push，min_stack则push进目前stack的最小值
  • 每次pop的时候，stack和min_stack都要执行pop操作

看个动图就能搞懂：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class MinStack {

    public ArrayDeque<Integer> stack;
    public ArrayDeque<Integer> min_stack;  // 辅助栈(用来实现getMin方法)

    public MinStack() {
        stack = new ArrayDeque<Integer>();
        min_stack = new ArrayDeque<Integer>();
        min_stack.addLast(Integer.MAX_VALUE);  // 初始化的时候就push一个Max值，方便后续操作
    }
    
    public void push(int val) {
        stack.addLast(val);
        min_stack.addLast(Math.min(val,min_stack.getLast()));  // 辅助栈push stack中最小的值
    }
    
    public void pop() {
        stack.removeLast();
        min_stack.removeLast();
    }
    
    public int top() {
        return stack.getLast();
    }
    
    public int getMin() {
        return min_stack.getLast();
    }
}

单链表

搬运自英文网站的高票解。

链表的节点包含以下信息：

  • 该节点值value
  • 该节点及以后（类似于栈中从某元素到栈底）的最小值min
  • 节点指向的下一个节点next

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class MinStack {

    class Node{
        private int value;
        private int min;
        private Node next;

        public Node() {
        }
        public Node(int value, int min) {
            this(value,min,null);
        }
        public Node(int value, int min, Node next) {
            this.value = value;
            this.min = min;
            this.next = next;
        }
    }
    private Node head;

    public MinStack() { // 这里什么都不要做，不要初始化head！
    }
    
    public void push(int val) {
        if (head==null){    // 栈为空，直接push，min即为该节点的value
            head = new Node(val,val);
        }else { // 栈已经有元素了，需要判断一下min该怎么取
            head = new Node(val, Math.min(val, head.min),head);
        }
    }
    
    public void pop() {
        head = head.next;
    }
    
    public int top() {
        return head.value;
    }
    
    public int getMin() {
        return head.min;
    }
}

160. 相交链表

LeetCode 160. 相交链表

哈希表

使用哈希表是可以过的，思路比较清晰，但是效率比较低下。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode p1 = headA;
        ListNode p2 = headB;
        Set<ListNode> set = new HashSet<>();
        while (p1!=null){
            set.add(p1);
            p1 = p1.next;
        }
        while (p2!=null){
            if (set.contains(p2)){
                return p2;
            }
            p2 = p2.next;
        }
        return null;

    }
}

复杂度分析：

  • 时间复杂度：O(m+n)。m和n分别为链表headA和headB的长度。
  • 空间复杂度：O(m)。m为链表headA的长度.需要用哈希表来存储headA链表的全部节点。

结果如下：解答成功:执行耗时:5 ms,击败了24.12% 的Java用户，内存消耗:44.2 MB,击败了32.56% 的Java用户

双指针（空间复杂度O(1)）

官方题解

其实原理很好懂，就是可能很难想到。（a+b=b+a）

首先定义两个指针p1，p2，分别指向headA和headB。特殊情况判断：当p1或者p2为空时，两个链表肯定不会相交，返回null。

接下来开始遍历p1，p2指针：

  • 当p1和p2指向的节点一样时，说明两个链表相交了；
  • 当p1为空时，p1指向headB；
  • 当p2为空时，p2指向headA；
  • 当p1和p2节点下一个都为空时，遍历结束，说明两个链表没有相交，返回null。

思路很好理解，画一下图甚至看一下图就能搞懂了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA==null || headB==null){
            return null;
        }
        ListNode p1 = headA;
        ListNode p2 = headB;
        while (p1!=null || p2!=null){
            if (p1==null){
                p1 = headB;
            }
            if (p2==null){
                p2 = headA;
            }
            if (p1==p2){
                return p1;
            }
            p1 = p1.next;
            p2 = p2.next;
        }
        return null;
    }
}

复杂度分析：

  • 时间复杂度：O(m+n)。m和n分别为链表headA和headB的长度。
  • 空间复杂度：O(1)。

结果为：解答成功:执行耗时:1 ms,击败了99.16% 的Java用户，内存消耗:44.6 MB,击败了5.12% 的Java用户

169. 多数元素

LeetCode 169. 多数元素

HashMap

一看到要统计数组各个数出现次数的相关题目，第一想法就是使用HashMap。这题使用HashMap的思路也比较简单。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int majorityElement(int[] nums) {
        int ans = 0;
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            if (map.containsKey(num)){
                map.put(num,map.get(num)+1);
            }else {
                map.put(num,1);
            }
        }
        Set<Map.Entry<Integer, Integer>> entries = map.entrySet();
        for (Map.Entry<Integer, Integer> entry : entries) {
            if (entry.getValue()>nums.length/2){
                ans = entry.getKey();
                return ans;
            }
        }
        return ans;
    }
}

结果为：解答成功:执行耗时:13 ms,击败了20.52% 的Java用户,内存消耗:46.6 MB,击败了4.99% 的Java用户

分治算法

官方题解

数学知识：如果数 a 是数组 nums 的众数，如果我们将 nums 分成两部分，那么 a 必定是至少一部分的众数。如果数 a 是数组 nums 的众数，如果我们将 nums 分成两部分，那么 a 必定是至少一部分的众数。

我们可以使用反证法来证明这个结论。假设 a 既不是左半部分的众数，也不是右半部分的众数，那么 a 出现的次数少于 l / 2 + r / 2 次，其中 l 和 r 分别是左半部分和右半部分的长度。由于 l / 2 + r / 2 <= (l + r) / 2，说明 a 也不是数组 nums 的众数，因此出现了矛盾。所以这个结论是正确的。

这样以来，我们就可以使用分治法解决这个问题：将数组分成左右两部分，分别求出左半部分的众数 a1 以及右半部分的众数 a2，随后在 a1 和 a2 中选出正确的众数。

我们使用经典的分治算法递归求解，直到所有的子问题都是长度为 1 的数组。

  • 长度为 1 的子数组中唯一的数显然是众数，直接返回即可。
  • 如果回溯后某区间的长度大于 1，我们必须将左右子区间的值合并：
    • 如果它们的众数相同，那么显然这一段区间的众数是它们相同的值；
    • 否则，我们需要比较两个众数在整个区间内出现的次数来决定该区间的众数。

初看比较绕，结合草稿和代码应该会比较清晰了：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    public int majorityElement(int[] nums) {
        return majorityElementRec(nums,0,nums.length-1);
    }

    /**
     * 分治法递归实现
     * @param nums 题目所给数组
     * @param l 左边开始索引
     * @param r 右边结束索引
     * @return 返回l-r区间内的多数元素
     */
    private int majorityElementRec(int[] nums, int l, int r) {
        if (l==r){  // base case，只有一个元素就返回这个元素
            return nums[l];
        }
        // 不止一个元素，就进行分治
        int mid = (r - l) / 2 + l;  // 分治后的中间位置索引
        int left = majorityElementRec(nums, l, mid);    // 左区间多数元素
        int right = majorityElementRec(nums, mid+1, r);    // 右区间多数元素
        if (left==right){   // 两个区间多数元素相等，则合并后的区间多数元素也是这个
            return right;
        }
        // 两个区间多数元素不相等，那么就要比较合并后的区间中这两个数哪个更多了
        int leftCount = countInRange(nums,left,l,r);
        int rightCount = countInRange(nums,right,l,r);
        return leftCount>rightCount? left:right;
    }

    /**
     * 统计一段区间内某个数出现的次数
     * @param nums 所给数组
     * @param num 所指定的数
     * @param l 区间左边索引
     * @param r 区间右边索引
     * @return 返回该数在该区间的出现次数
     */
    private int countInRange(int[] nums, int num, int l, int r) {
        int count = 0;
        for (int i = l; i <= r; i++) {
            if (nums[i]==num){
                count++;
            }
        }
        return count;
    }
}

结果为：解答成功:执行耗时:1 ms,击败了99.92% 的Java用户,内存消耗:44.6 MB,击败了26.50% 的Java用户

179. 最大数

LeetCode 179. 最大数

贪心+优先队列

由宫水三叶大佬提供的题解。

对于 numsnums 中的任意两个值 aa 和 bb，我们无法直接从常规角度上确定其大小/先后关系。但我们可以根据「结果」来决定 aa 和 bb 的排序关系：

如果拼接结果 abab 要比 baba 好，那么我们会认为 aa 应该放在 bb 前面。

另外，注意我们需要处理前导零（最多保留一位）。

这题如果没有想到好的方向，似乎挺难的。但是如果想对方向了，似乎思路也挺简单的。

这题主要用到的数据结构为优先队列，贪心思想主要体现在自定义比较器Comparator中。

根据结果来确定排序，直接上代码吧：

1
2
3
4
5
6
7
8
9
10
// 自定义排序规则
Comparator<String> comparator = new Comparator<String>() {
    @Override
    public int compare(String s1, String s2) {
        String o1 = s1 + s2;
        String o2 = s2 + s1;
        // o2.compareTo(o1)>0，说明字符串o2大于o1，s1和s2要交换顺序(实现类似降序排列)
        return o2.compareTo(o1);
    }
};

给个例子：

排序规则写好后，使用优先队列来求解就非常简单了：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public String largestNumber(int[] nums) {
        StringBuilder stringBuilder = new StringBuilder();
        // 自定义排序规则
        Comparator<String> comparator = new Comparator<String>() {
            @Override
            public int compare(String s1, String s2) {
                String o1 = s1 + s2;
                String o2 = s2 + s1;
                // o2.compareTo(o1)>0，说明字符串o2大于o1，s1和s2要交换顺序(实现类似降序排列)
                return o2.compareTo(o1);
            }
        };
        PriorityQueue<String> priorityQueue = new PriorityQueue<>(comparator);
        for (int num : nums) {  // 入队
            priorityQueue.add(String.valueOf(num));
        }
        for (int i = 0; i < nums.length; i++) {
            stringBuilder.append(priorityQueue.poll());
        }
        // 下面的处理是为了消去结果前面的0，比如说测试用例：[0,0,0],应该返回0而不是000
        String s = new String(stringBuilder);
        int k = 0;
        while (stringBuilder.charAt(k)=='0'&&k<stringBuilder.length()-1){
            k++;
        }
        // 循环结束后k即为第一个非0字符所在索引
        return stringBuilder.substring(k);
    }
}
  • 时间复杂度：由于是对 StringString 进行排序，当排序对象不是 JavaJava 中的基本数据类型时，不会使用快排（考虑排序稳定性问题）。Arrays.sort() 的底层实现会「元素数量/元素是否大致有序」决定是使用插入排序还是归并排序。这里直接假定使用的是「插入排序」。复杂度为 O(n^2)
  • 空间复杂度：O(n)

我最开始是看的开心大佬提供的题解，打下草稿发现大致思路跟上面一样

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    public String largestNumber(int[] nums) {
        StringBuilder stringBuilder = new StringBuilder();
        // 自定义排序规则
        Comparator<String> comparator = new Comparator<String>() {
            @Override
            public int compare(String s1, String s2) {
                char a,b;
                for (int i = 0; i < s1.length()+s2.length(); i++) {
                    if (i<s1.length()){
                        a = s1.charAt(i);
                    }else {
                        a = s2.charAt(i-s1.length());
                    }
                    if (i<s2.length()){
                        b = s2.charAt(i);
                    }else {
                        b = s1.charAt(i-s2.length());
                    }
                    if (a!=b){ // 在从第一位比较的过程中，只要发现a和b不相同，return b-a
                        return b-a;     // 按照(类似)降序排列，所以是b-a
                    }
                }
                return 0;   // 循环结束后还没有判断出s1和s2的排序，return 0
            }
        };
        PriorityQueue<String> priorityQueue = new PriorityQueue<>(comparator);
        for (int num : nums) {  // 入队
            priorityQueue.add(String.valueOf(num));
        }
        for (int i = 0; i < nums.length; i++) {
            stringBuilder.append(priorityQueue.poll());
        }
        String s = new String(stringBuilder);
        if (s.charAt(0)=='0'){  // 对于特殊用例：[0,0]，应该输出0而不是00
            return "0";
        }
        return s;
    }
}
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

191. 位1的个数

LeetCode 191. 位1的个数

位运算

这题在写过LeetCode 1601. 最多可达成的换楼请求数目之后就非常简单了。在那题中，此题只是其中一个方法。

观察这个运算： n&(n−1)n \&(n-1) ，其运算结果恰为把 nn 的二进制位中的最低位的 1 变为 0 之后的结果。
如: 6&(6−1)=4,6=(110)2,4=(100)26 \&(6-1)=4,6=(110)_{2}, 4=(100)_{2} ，运算结果 4 即为把 6 的二进制位中的最低位的 1 变为 0 之后 的结果。

在位运算中用到了lowbit 运算。具体体现在：

1
2
3
for (int i = num; i != 0; i = i&(i-1)) {
    count++;
}

lowbit还有另一种写法：

1
2
3
for (int i = num; i != 0; i = i-(i&-i)) {
    count++;
}

【位运算】深入理解并证明 lowbit 运算

代码如下：

1
2
3
4
5
6
7
8
9
10
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count = 0;
        for (int i = n; i != 0; i = i&(i-1)) {
            count++;
        }
        return count;
    }
}

200. 岛屿数量

LeetCode 200. 岛屿数量

深度优先搜索（DFS）

岛屿类问题的通用解法、DFS 遍历框架

具体思路大佬题解中已经说的非常详细了，这里注意一下：

  • 0：海洋格子
  • 1：陆地格子（未遍历过）
  • 2：陆地格子（已遍历过）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    public int numIslands(char[][] grid) {
        int count = 0;
        // 双层for循环，其实就是遍历每一个网格(r行c列)
        for (int r = 0; r < grid.length; r++) {
            for (int c = 0; c < grid[0].length; c++) {
                if (grid[r][c]=='1'){
                    dfs(grid,r,c);  // 发现还未遍历过的陆地，开始深度优先搜索进行遍历
                    count++;    // 深度优先搜索结束后，岛屿数量+1
                }
            }
        }
        return count;
    }

    /**
     * 网格的深度优先搜索
     */
    private void dfs(char[][] grid, int r, int c) {
        // 判断 base case
        // 如果坐标 (r, c) 超出了网格范围，直接返回
        // 如果不是陆地，也直接返回
        if (!inArea(grid, r, c) || grid[r][c]=='0' || grid[r][c]=='2'){
            return;
        }
        grid[r][c] = '2';     // 标记为已经遍历过的陆地
        // 开始网格的深度优先搜索（上下左右）
        dfs(grid, r-1, c);
        dfs(grid, r+1, c);
        dfs(grid, r, c-1);
        dfs(grid, r, c+1);
    }

    /**
     * 判断坐标(r,c)是否超出了grid的范围
     * @return
     */
    private boolean inArea(char[][] grid, int r, int c) {
        return (r>=0 && r<grid.length) && (c>=0 && c<grid[0].length);
    }
}

203. 移除链表元素

LeetCode 203. 移除链表元素

双指针

首先还是定义dummyNode，dummyNode.next = head;。这种处理在单链表中已经是很常见了（即区别于头结点和首元节点）。

定义两个指针。p1初始指向dummyNode，p2初始指向head。接下来p2开始遍历单链表知道尽头：

  • 如果p2所指节点的val不为指定值：p1和p2都向后移动一个节点
  • 如果p2所指节点的val为指定值：p2继续移动直到p2所指节点不为val，此时令p1.next = p2。

打下草稿就能搞懂。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        ListNode dummyNode = new ListNode();
        dummyNode.next = head;
        ListNode p1 = dummyNode;
        ListNode p2 = head;
        while (p2!=null){
            if (p2.val!=val){
                p1 = p1.next;
                p2 = p2.next;
            }else {
                while (p2!=null && p2.val == val){
                    p2 = p2.next;
                }
                p1.next = p2;
            }
        }
        return dummyNode.next;
    }
}

206. 反转链表

LeetCode 206. 反转链表

单链表

反转链表在之前的数据结构学习中就已经实现过了，可以参考笔记。这题本身也是个简单题，直接给出代码吧：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null;
        ListNode cur = head;
        while (cur!=null){
            ListNode next = cur.next;
            cur.next = pre; // 修改结点指向
            pre = cur;
            cur = next;
        }
        return pre;
    }
}

215. 数组中的第K个最大元素

LeetCode 215. 数组中的第K个最大元素

217. 存在重复元素

哈希表

这题使用哈希表来求解，思路就非常简单了。直接给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public boolean containsDuplicate(int[] nums) {
        Arrays.sort(nums);  // 将nums按升序排序
        HashSet<Integer> hashSet = new HashSet<>();
        for (int i = 0; i < nums.length; i++) {
            /* 若向HashSet中插入重复元素，则返回false
            hashSet.add(nums[i])为真，即没有重复元素
            所以我们条件为!hashSet.add(nums[i])，有重复元素，返回true*/
            if (!hashSet.add(nums[i])){
                return true;
            }
        }
        return false;
    }
}

最开始我是这么写的：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public boolean containsDuplicate(int[] nums) {
        Arrays.sort(nums);  // 将nums按升序排序
        HashSet<Integer> hashSet = new HashSet<>();
        for (int i = 0; i < nums.length; i++) {
            if (hashSet.contains(nums[i])){
                return true;
            }
            hashSet.add(nums[i]);
        }
        return false;
    }
}

但是运行结果为：解答成功:执行耗时:9 ms,击败了7.65% 的Java用户，内存消耗:43.9 MB,击败了37.45% 的Java用户。于是我把代码改成上述代码，结果为：解答成功:执行耗时:7 ms,击败了29.90% 的Java用户，内存消耗:42.6 MB,击败了40.24% 的Java用户。

225. 用队列实现栈

LeetCode 225. 用队列实现栈

队列

比较简单。主要是要熟悉队列和栈这种数据结构，以及在Java中对应的集合类。通常，我们在Java中都会用ArrayDeque来实现栈和队列。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class MyStack {
    private ArrayDeque<Integer> deque;

    public MyStack() {
       deque = new ArrayDeque<>();
    }
    
    public void push(int x) {
        deque.add(x);
    }
    
    public int pop() {
        return deque.removeLast();
    }
    
    public int top() {
        return deque.getLast();
    }
    
    public boolean empty() {
        return deque.isEmpty();
    }
}

226. 翻转二叉树

LeetCode 226. 翻转二叉树

232. 用栈实现队列

LeetCode 232. 用栈实现队列

栈(入队：O(n)， 出队：O(1))

入队：O(n)， 出队：O(1)

用栈来实现队列，只是在push的时候有点麻烦，需要用到一个辅助栈。处理push的逻辑目的只有一个：要保证栈顶是队头，栈底是队尾。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class MyQueue {
    private ArrayDeque<Integer> deque;  // 在后面的逻辑中，要保证栈顶是队头，栈底是队尾

    public MyQueue() {
        deque = new ArrayDeque<>();
    }
    
    public void push(int x) {
        ArrayDeque<Integer> deque2 = new ArrayDeque<>();    // 辅助栈
        while (!deque.isEmpty()){
            deque2.push(deque.pop());
        }
        // 然后将x元素push到deque中，这是x即为deque队尾
        deque.push(x);
        // 最后将辅助栈中的元素push回deque中
        while (!deque2.isEmpty()){
            deque.push(deque2.pop());
        }
    }
    
    public int pop() {
        return deque.pop();
    }
    
    public int peek() {
        return deque.peek();
    }
    
    public boolean empty() {
        return deque.isEmpty();
    }
}

栈（进阶：入队：O(1)，出队：摊还复杂度 O(1)）

入队：O(1)，出队：摊还复杂度 O(1)

来自官方题解提供的方法二。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class MyQueue {
    private ArrayDeque<Integer> deque1;
    private ArrayDeque<Integer> deque2;
    private int front;  // 队头元素

    public MyQueue() {
        deque1 = new ArrayDeque<>();
        deque2 = new ArrayDeque<>();

    }
    
    public void push(int x) {
        if (deque1.isEmpty()){
            front = x;
        }
        deque1.push(x);
    }
    
    public int pop() {
        if (deque2.isEmpty()) {
            while (!deque1.isEmpty())
                deque2.push(deque1.pop());
        }
        return deque2.pop();
    }
    
    public int peek() {
        if (!deque2.isEmpty()){
            return deque2.peek();
        }
        return front;
    }
    
    public boolean empty() {
        return deque1.isEmpty()&& deque2.isEmpty();
    }
}

239. 滑动窗口最大值

LeetCode 239. 滑动窗口最大值

单调队列

关于单调队列这种数据结构，我们在之前的笔记中有简单提到过。单调队列经常用来解决数组滑动窗口的最值问题。

动画演示 单调队列 239.滑动窗口最大值

大佬给出的题解中动画演示已经非常清晰了，这里给出关键的总结如下：

  • 遍历给定数组中的元素，如果队列不为空且当前考察元素大于等于队尾元素，则将队尾元素移除（pollLast()）。直到，队列为空或当前考察元素小于新的队尾元素（要保证是单调递减队列）；
  • 当队首元素的下标小于滑动窗口左侧边界left时，表示队首元素已经不再滑动窗口内，因此将其从队首移除。（poll() ）
  • 由于数组下标从0开始，因此当窗口右边界right+1大于等于窗口大小k时，意味着窗口形成。此时，队首元素就是该窗口内的最大值。（peek()）

注意：在单调队列中，我们存储的不是nums数组中元素的值，而是nums元素的下标值！

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int[] result = new int[nums.length - k + 1];
        // 用LinkedList来实现双端队列
        LinkedList<Integer> deque = new LinkedList<>();
        // 定义左下标和右下标
        int left = 0;
        int right;
        // 下面的代码中，left表示左下标，right表示右下标
        for (right = 0; right < nums.length; right++) {
            // 如果队列不为空且当前考察元素大于等于队尾元素，则将队尾元素移除。
            // 直到，队列为空或当前考察元素小于新的队尾元素
            // 注意这里要用while而不是if,因为要保证是单调递减队列
            while (!deque.isEmpty()&&nums[right]>=nums[deque.peekLast()]){
                deque.pollLast();
            }
            deque.addLast(right); // 存储符合规则的元素下标,注意这里存储的是元素下标
            // 如果右下标right大于等于k-1，说明窗口形成(当right为k-1时，left正好为0)
            if (right>=k-1){
                // 当队首元素的下标小于滑动窗口左侧边界left时，表示队首元素已经不再滑动窗口内，因此将其从队首移除
                if (deque.peek()<left){
                    deque.poll();
                }
                // 不满足上述if条件，则说明队首元素的下标是在窗口内，而我们又保证了该队列是单调递减队列
                // 直接将队首元素放到result数组中即可
                result[left] = nums[deque.peek()];
                // 当窗口形成后，right++的同时left也要++
                left++;
            }
        }
        return result;
    }
}

结果为：解答成功:执行耗时:27 ms,击败了93.78% 的Java用户，内存消耗:49.9 MB,击败了99.23% 的Java用户

242. 有效的字母异位词

LeetCode 242. 有效的字母异位词

数组

全是小写字母，使用数组来处理这种方式已经非常熟悉了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean isAnagram(String s, String t) {
        int[] arr_s = new int[26];
        int[] arr_t = new int[26];
        for (int i = 0; i < s.length(); i++) {
            arr_s[s.charAt(i)-'a']++;
        }
        for (int i = 0; i < t.length(); i++) {
            arr_t[t.charAt(i)-'a']++;
        }
        for (int i = 0; i < 26; i++) {
            if (arr_s[i]!=arr_t[i]){
                return false;
            }
        }
        return true;
    }
}

258. 各位相加

LeetCode 258. 各位相加

模拟

根据题意，将给定的num的各个位的值一个一个相加即可。这里的代码处理是：先将num%10得到最低位，然后num = num/10。直到num为0。思路很清晰，主要就是代码实现num的每一位的相加。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int addDigits(int num) {
        while (num>=10){    // 需要进行各位的相加
            int temp = 0;
            while (num>0){  // num各位相加的代码实现
                temp = temp+num%10;
                num = num/10;
            }
            num = temp; // num更新为各位相加之后的值
        }
        return num;
    }
}

复杂度分析：

  • 时间复杂度：O(logn)。n为给定的num值。对于num 计算一次各位相加需要 O(logn) 的时间，由于num ≤231−1\leq 2^{31}-1，因此对于 num 计算一次各位相加的最大可能结果是 82，对于任意两位数最多只需要计算两次各位相加的结果即可得到一位数。
  • 空间复杂度：O(1)

数学（双O(1)）

官方题解

这道题的本质是计算自然数num的数根。

数根又称数字根（Digital root），是自然数的一种性质，每个自然数都有一个数根。对于给定的自然数，反复将各个位上的数字相加，直到结果为一位数，则该一位数即为原自然数的数根。

我们利用自然数的性质，则能在 O(1) 的时间内计算数根。

假设整数 numn u m 的十进制表示有 nn 位，从最低位到最高位依次是 a0a_{0} 到 an−1a_{n-1} ，则 numn u m 可以 写成如下形式:

 num =∑i=0n−1ai×10i=∑i=0n−1ai×(10i−1+1)=∑i=0n−1ai×(10i−1)+∑i=0n−1ai\begin{aligned} \text { num } &=\sum_{i=0}^{n-1} a_{i} \times 10^{i} \\ &=\sum_{i=0}^{n-1} a_{i} \times\left(10^{i}-1+1\right) \\ &=\sum_{i=0}^{n-1} a_{i} \times\left(10^{i}-1\right)+\sum_{i=0}^{n-1} a_{i} \end{aligned}

当 i=0i=0 时， 10i−1=010^{i}-1=0 是 9 的倍数；当 ii 是正整数时， 10i−110^{i}-1 是由 ii 位 9 组成的整数， 也是 9 的倍数。因此对于任意非负整数 i,10i−1i, 10^{i}-1 都是 9 的倍数。由此可得 numn u m 与其各位相加的结果模 9 同余。（即num和num各位之和%9的结果是一样的。比如说：38%9=2,11%9=2）

重复计算各位相加的结果直到结果为一位数时，该一位数即为 numn u m 的数根，num 与其数根模 9 同余。

我们对 num 分类讨论：

  • num 不是 9 的倍数时，其数根即为 num 除以 9 的余数。
  • num 是 9 的倍数时：
    • 如果 num=0n u m=0 ，则其数根是 0 ；
    • 如果 num>0n u m>0 ，则各位相加的结果大于 0 ，其数根也大于 0 ，因此其数根是 9

代码如下：

1
2
3
4
5
6
7
8
9
class Solution {
    public int addDigits(int num) {
        if (num%9!=0){  // num不是9的倍数
            return num%9;
        }else {
            return num==0? 0:9;
        }
    }
}

316. 去除重复字母

LeetCode 316. 去除重复字母

注意：该题与1081. 不同字符的最小子序列相同。

单调栈

官方题解（含视频）

这题感觉如果没有正确的方向的话是挺难的。官方提供的题解已经说的很好了，这里我用自己的语言分析一下。

要解决这个问题，需要用到：

  • 一个单调栈：为什么要用单调栈呢，因为要保证栈中的结果永远都是字典序最小
  • 两个数组：lastIndex数组存储字符串s中各个字母出现的最后一个位置，visited数组存储各个字符是否已经存在于栈中

接下来就可以遍历字符串s，分析一下单调栈的存储过程：

  • 首先，先判断当前字符是否已经存在于栈中，如果已经存在，什么都不做开始遍历下一个字符（continue）

  • 如果该字符不存在与栈中（这里用while）：

    • 那么就先判断遍历的字符是否大于栈顶元素top，如果遍历的字符大于栈顶字符top，那么就无需执行下面的操作，直接跳出while循环

    • 如果字符小于栈顶元素top，那么就先判断栈的栈顶元素top是否还会再次出现（i<lastIndex[top-'a']），如果top字符在字符串s后面的遍历中还会出现的话，那么就pop出该栈顶元素，同时在visited数组中设置该字符不存在于栈中（visited[top-'a']=false）

      。接着继续拿遍历的字符跟新的栈顶元素进行上述比较（同样要先判断遍历的字符是否大于栈顶元素top，再判断栈的栈顶元素top是否还会再次出现）（这么做是为了保证栈中的结果永远都是字典序最小，所以要用while）

    • while循环结束后，将该字符push到栈中，同时在visited数组中设置该字符已经存在于栈中

      （visited[charArray[i]-'a']=true）

  • 字符串s遍历之后，栈中从栈底到栈顶的顺序即为我们的结果

光看文字描述可能很迷糊，但光看代码也会很迷糊，文字结合代码一起看应该就比较清晰了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public String removeDuplicateLetters(String s) {
        int length = s.length();
        char[] charArray = s.toCharArray();
        // 一个单调栈，两个数组
        ArrayDeque<Character> stack = new ArrayDeque<>();
        // 题目已经说了都是小写，所以长度为26
        int[] lastIndex = new int[26];  // 存储字符串中字母出现的最后一个位置
        boolean[] visited = new boolean[26];    // 存储a-z这26个字母是否已经存在于栈中
        // 这个循环结束后，lastIndex数组即成功存储到a-z(0-25)的字母在字符串s中出现的最后位置
        for (int i = 0; i < length; i++) {
            lastIndex[charArray[i]-'a']=i;
        }
        // 准备工作都已完毕，接下来就可以开始遍历字符串s了
        for (int i = 0; i < length; i++) {
            if (visited[charArray[i]-'a']){ // 字母已经存在与栈中，直接continue
                continue;
            }
            // 注意while循环中还要加上stack不为空
            while (!stack.isEmpty() && charArray[i]<stack.peekLast() && i<lastIndex[stack.peekLast()-'a']){
                Character top = stack.removeLast();
                visited[top-'a'] = false;
            }
            stack.addLast(charArray[i]);
            visited[charArray[i]-'a'] = true;
        }
        // 遍历结束后，栈中结果即字典序最小
        // 因为我们使用ArrayDeque来模拟栈，所以当然可以直接遍历ArrayDeque
        StringBuilder stringBuilder = new StringBuilder();
        for (Character character : stack) {
            stringBuilder.append(character);
        }
        return stringBuilder.toString();
    }
}
  • 时间复杂度：O(n)，n为字符串s的长度
  • 空间复杂度：O(n)，栈的最大深度

341. 扁平化嵌套列表迭代器

LeetCode 341. 扁平化嵌套列表迭代器

深度优先搜索（DFS）

官方题解

关键要看懂题目给定的接口NestedInteger。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// This is the interface that allows for creating nested lists.
// You should not implement it, or speculate about its implementation
public interface NestedInteger {
    // @return true if this NestedInteger holds a single integer, rather than a nested list.
    public boolean isInteger();
    
    // @return the single integer that this NestedInteger holds, if it holds a single integer
    // Return null if this NestedInteger holds a nested list
    public Integer getInteger();
    
    // @return the nested list that this NestedInteger holds, if it holds a nested list
     // Return empty list if this NestedInteger holds a single integer
    public List<NestedInteger> getList();
}

给定了三个方法：

  • public boolean isInteger()：如果是single integer，返回true；否则返回false
  • public Integer getInteger()：返回当前integer
  • public List<NestedInteger> getList()：返回当前list

搞清楚了这三个方法的作用，题解就很好写了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class NestedIterator implements Iterator<Integer> {
    private List<Integer> values;
    private Iterator<Integer> cur;

    public NestedIterator(List<NestedInteger> nestedList) {
        values = new ArrayList<Integer>();
        dfs(nestedList);
        cur = values.iterator();
    }

    private void dfs(List<NestedInteger> nestedList) {
        for (NestedInteger nestedInteger : nestedList) {
            if (nestedInteger.isInteger()){
                values.add(nestedInteger.getInteger());
            }else {
                dfs(nestedInteger.getList());
            }
        }
    }

    @Override
    public Integer next() {
        return cur.next();
    }

    @Override
    public boolean hasNext() {
        return cur.hasNext();
    }
}
  • 时间复杂度：dfs()为O(n)，next()和hasNext()为O(1)。其中n是嵌套的整形列表中的元素个数。
  • 空间复杂度：O(n)。需要一个数组存储嵌套的整形列表中的所有元素。

349. 两个数组的交集

LeetCode 349. 两个数组的交集

HashSet

用两个HashSet就能解决这个问题。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> set2 = new HashSet<>();
        List<Integer> list = new ArrayList<>();
        for (int num : nums1) {
            set1.add(num);
        }for (int num : nums2) {
            set2.add(num);
        }
        int size1 = set1.size();
        int size2 = set2.size();
        if (size1>size2){
            for (Integer integer : set1) {
                if (set2.contains(integer)){
                    list.add(integer);
                }
            }
        }else {
            for (Integer integer : set2) {
                if (set1.contains(integer)){
                    list.add(integer);
                }
            }
        }
        int[] ans = new int[list.size()];
        for (int i = 0; i < ans.length; i++) {
            ans[i] = list.get(i);
        }
        return ans;
    }
}

350. 两个数组的交集 II

LeetCode 350. 两个数组的交集 II

HashMap

使用两个HashMap解决。思路也比较清晰，key表示数组中的元素，value表示该元素在数组中出现的次数。可能代码看起来比较麻烦。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        List<Integer> list = new ArrayList<>();
        Map<Integer, Integer> map1 = new HashMap<>();
        Map<Integer, Integer> map2 = new HashMap<>();
        for (int num : nums1) {
            if (map1.containsKey(num)){
                map1.put(num,map1.get(num)+1);
            }else {
                map1.put(num,1);
            }
        }
        for (int num : nums2) {
            if (map2.containsKey(num)){
                map2.put(num,map2.get(num)+1);
            }else {
                map2.put(num,1);
            }
        }
        int size1 = map1.size();
        int size2 = map2.size();
        if (size1>size2){
            for (Map.Entry<Integer, Integer> entry : map1.entrySet()) {
                if (map2.containsKey(entry.getKey())){
                    for (int i = 0; i < Math.min(entry.getValue(), map2.get(entry.getKey())); i++) {
                        list.add(entry.getKey());
                    }
                }
            }
        }else {
            for (Map.Entry<Integer, Integer> entry : map2.entrySet()) {
                if (map1.containsKey(entry.getKey())){
                    for (int i = 0; i < Math.min(entry.getValue(), map1.get(entry.getKey())); i++) {
                        list.add(entry.getKey());
                    }
                }
            }
        }
        int[] ans = new int[list.size()];
        for (int i = 0; i < ans.length; i++) {
            ans[i] = list.get(i);
        }
        return ans;
    }
}

我自己写的比较繁琐，下面看一下官方题解。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        if (nums1.length > nums2.length) {
            return intersect(nums2, nums1);
        }
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums1) {
            int count = map.getOrDefault(num, 0) + 1;
            map.put(num, count);
        }
        int[] ans = new int[nums1.length];
        int index = 0;
        for (int num : nums2) {
            int count = map.getOrDefault(num, 0);
            if (count > 0) {
                ans[index] = num;
                index++;
                count--;
                if (count > 0) {
                    map.put(num, count);
                } else {
                    map.remove(num);
                }
            }
        }
        return Arrays.copyOfRange(ans, 0, index);
    }
}

复杂度分析：

  • 时间复杂度：O(m+n)，其中 m和 n 分别是两个数组的长度。需要遍历两个数组并对哈希表进行操作，哈希表操作的时间复杂度是 O(1)，因此总时间复杂度与两个数组的长度和呈线性关系。
  • 空间复杂度：空间复杂度：O(min(m,n))，其中 m 和 n 分别是两个数组的长度。对较短的数组进行哈希表的操作，哈希表的大小不会超过较短的数组的长度。为返回值创建一个数组 ans，其长度为较短的数组的长度。

排序+双指针

对应进阶提问中：如果给定的数组已经排好序呢？你将如何优化你的算法？

官方题解

如果两个数组是有序的，则可以使用双指针的方法得到两个数组的交集。

首先对两个数组进行排序，然后使用两个指针遍历两个数组。

初始时，两个指针分别指向两个数组的头部，每次比较两个指针指向的两个数组中的数字：

  • 如果两个数字不相等，则将指向较小数字的指针右移一位
  • 如果两个数字相等，将该数字添加到答案，并将两个指针都右移一位
  • 当至少有一个指针超出数组范围时，遍历结束

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        List<Integer> list = new ArrayList<>();
        Arrays.sort(nums1);
        Arrays.sort(nums2);
        // 双指针
        int i = 0;
        int j = 0;
        while (i<nums1.length && j<nums2.length){
            if (nums1[i]==nums2[j]){
                list.add(nums1[i]);
                i++;
                j++;
            }else if (nums1[i]<nums2[j]){
                i++;
            }else {
                j++;
            }
        }
        int[] ans = new int[list.size()];
        for (int index = 0; index < ans.length; index++) {
            ans[index] = list.get(index);
        }
        return ans;
    }
}

复杂度分析：

  • 时间复杂度：O(mlogm+nlogn)。其中 m 和 n 分别是两个数组的长度。对两个数组进行排序的时间复杂度是 O(mlogm+nlogn)，遍历两个数组的时间复杂度是 )O(m+n)，因此总时间复杂度是 O(mlogm+nlogn)。
  • 空间复杂度：O(min(m,n))。其中 m 和 n 分别是两个数组的长度。

383. 赎金信

LeetCode 383. 赎金信

数组

题目已经说明了字符均为小写字母，巧妙地使用ASCII码即可。这种方法也已经非常熟悉了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean canConstruct(String ransomNote, String magazine) {
        int[] arr_ran = new int[26];
        int[] arr_mag = new int[26];
        for (int i = 0; i < ransomNote.length(); i++) {
            arr_ran[ransomNote.charAt(i)-'a']++;
        }
        for (int i = 0; i < magazine.length(); i++) {
            arr_mag[magazine.charAt(i)-'a']++;
        }
        for (int i = 0; i < 26; i++) {
            if (arr_ran[i]>arr_mag[i]){
                return false;
            }
        }
        return true;
    }
}

387. 字符串中的第一个唯一字符

LeetCode 387. 字符串中的第一个唯一字符

LinkedHashMap

这里之所以用LinkedHashMap，是因为LinkedHashMap是有序的，方便找出第一个不重复的字符的索引。

原理很简单看代码就能搞懂，注意一下我们的LinkedHashMap，key为字符，value为字符在字符串中的索引即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int firstUniqChar(String s) {
        // key存储字符，value存储字符在字符串中的索引
        // 我们需要Map有序所以使用了LinkedHashMap
        LinkedHashMap<Character, Integer> linkedHashMap = new LinkedHashMap<>();
        for (int i = 0; i < s.length(); i++) {
            char ch = s.charAt(i);
            if (linkedHashMap.containsKey(ch)){   // key已经有该字符了，说明是重复的
                linkedHashMap.put(ch,-1); // 将其value置为-1
            }else { // 不重复
                linkedHashMap.put(ch,i);
            }
        }
        // LinkedHashMap是有序的，所以我们遇到了第一个value不为-1的即为第一个不重复字符所在的索引
        for (Map.Entry<Character, Integer> entry : linkedHashMap.entrySet()) {
            if (entry.getValue()!=-1){
                return entry.getValue();
            }
        }
        return -1;
    }
}

数组计数（高效率）

来自汪雪雷大佬提供的题解。

题目已经说明了字符均为小写字母，我们可以巧妙地使用ASCII码。

具体思路只要看一眼代码就能搞懂。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int firstUniqChar(String s) {
        // arr用来存储a，b，c等26个字母出现的次数
        int[] arr = new int[26];    // 因为只有26个小写字母
        for (int i = 0; i < s.length(); i++) {
            arr[s.charAt(i)-'a']++; // 举个例子，若字符为c，则为arr[2]++
        }
        // arr数组存储完毕后，就可以开始遍历s了
        for (int i = 0; i < s.length(); i++) {
            if (arr[s.charAt(i)-'a']==1){   // 为0表示没有出现，为1则为只出现一次
                return i;
            }
        }
        return -1;
    }
}

上面的LinkedHashMap用时22 ms，而此方法用时仅5 ms。

392. 判断子序列

LeetCode 392. 判断子序列

双指针

首先搞清楚子序列的定义，接下来代码就比较好写了。

草稿如下：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public boolean isSubsequence(String s, String t) {
        int length_s = s.length();
        int length_t = t.length();
        // 特殊情况判断
        if (length_s>length_t){
            return false;
        }else if (length_s==length_t){
            return s.equals(t);
        }else if (length_s==0){
            return true;
        }
        // 双指针，i指向t的开头，j指向s开头
        int i = 0;
        int j = 0;
        while (i<length_t){
            if (t.charAt(i)==s.charAt(j)){  // j继续向下遍历的条件
                j++;
            }
            if (j==length_s){ // 如果j走遍了字符串s，说明s是t的子序列
                return true;
            }
            i++;
        }
        return false;
    }
}

393. UTF-8 编码验证

LeetCode 393. UTF-8 编码验证

模拟（遍历+位运算）

这是一道模拟题，主要要搞懂UTF-8编码具体是如何验证的，可以参考这个视频来理解。

首先我们要搞清楚如何判断是哪种验证方法。题目给了如下四种验证方法：

1
2
3
4
5
6
7
Char. number range  |        UTF-8 octet sequence
      (hexadecimal)    |              (binary)
   --------------------+---------------------------------------------
   0000 0000-0000 007F | 0xxxxxxx
   0000 0080-0000 07FF | 110xxxxx 10xxxxxx
   0000 0800-0000 FFFF | 1110xxxx 10xxxxxx 10xxxxxx
   0001 0000-0010 FFFF | 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx

通过观察可以发现：

  • 第一个0在第1位，第一种验证方法
  • 第一个0在第3位，第二种验证方法
  • 第一个0在第4位，第三种验证方法
  • 第一个0在第5位，第四种验证方法

如何验证第一个0在第几位，需要使用到位运算（位与 &）。举个例子，判断数字num：

  • num & 128 = 0，第一个0在第1位
  • num & 64 = 0， 第一个0在第2位
  • num & 32 = 0， 第一个0在第3位
  • num & 16 = 0， 第一个0在第4位
  • num & 8 = 0， 第一个0在第5位

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    private int[] masks = new int[]{128,64,32,16,8};
    public boolean validUtf8(int[] data) {
        for (int i = 0; i < data.length; i++) {
            int index = get0Index(data[i]); // 获取当前数第一个0在第几位(注意返回的是masks数组下标，即返回0表示第一个0在第1位)
            if (index==0){  // 第一个0在第1位，肯定是合法的，直接continue
                continue;
            } else if (index>1 && i+index<=data.length){    // 第一个0在3,4,5位
                // 举个例子，index==3，第一个0在第4位，那么需要判断data[i]其后2个数是否合法（是否是10开头）
                while (index>1){    // 以index==3为例，i后两个data判断
                    i++;
                    if (get0Index(data[i])!=1){
                        return false;
                    }
                    index--;
                }
            }else { // 其他情况即为不合法情况，return false
                return false;
            }
        }
        return true;
    }

    /**
     * 判断给定数的第一个0在第几位
     * @param num 指定数
     * @return 返回第一个0在第几位（如1011即返回2）
     */
    private int get0Index(int num) {
        for (int i = 0; i < masks.length; i++) {
            if ((num&masks[i])==0){
                return i;
            }
        }
        return -1;
    }
}

415. 字符串相加

LeetCode 415. 字符串相加

模拟+双指针

这题主要是来模拟两个整数之间的竖式加法。一开始我以为要分好多种情况来区分num1和num2长度的不同，但其实只需要在高位进行补0操作即可。这里我们使用两个指针，初始分别指向num1和num2的末尾，然后从右到左来计算出num1和num2的值即可。

注意下代码中的三元表达式，意思其实就是高位补0：

1
2
3
// 这里使用三元表达式更加简洁
int x = i>=0? (num1.charAt(i)-'0'):0;
int y = j>=0? (num2.charAt(j)-'0'):0;

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public String addStrings(String num1, String num2) {
            StringBuffer result = new StringBuffer();
            // 两个指针，初始分别指向num1和num2的末尾
            int i = num1.length() - 1;
            int j = num2.length() - 1;
            int flag = 0;   // 是否进位标志
            while (i>=0 || j>=0 || flag!=0){
                // 这里使用三元表达式更加简洁
                int x = i>=0? (num1.charAt(i)-'0'):0;
                int y = j>=0? (num2.charAt(j)-'0'):0;
                int n = x + y + flag;
                result.append(n%10);
                flag = n/10;    // n<10，flag为0；n>10，flag为1
                i--;
                j--;
            }
            result.reverse();   // 别忘了结果要先反转
            return result.toString();
    }
}

455. 分发饼干

LeetCode 455. 分发饼干

贪心算法

分析：这题的贪心思想比较简单。先将g数组和s数组按升序排列后，再依次比较，判断 s[j] >= g[i]是否成立。成立则分配饼干给孩子吃，且孩子下标i和饼干下标j都+1；若不成立则仅将饼干下标j+1（因为已经将g数组和s数组排序过了。）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int findContentChildren(int[] g, int[] s) {
        int sum = 0;
        Arrays.sort(g); // 将g数组即孩子胃口数组从小到大排序
        Arrays.sort(s); // 将s数组即饼干尺寸数组从小到大排序
        int i=0,j=0;    // 后续遍历用
        while (i<g.length&&j<s.length){
            // 只是饼干下标增加，继续匹配
            if (s[j]>=g[i]){    // 可以吃
                sum++;
                i++;    // 孩子吃完饼干后，下标+1开始寻找下一个孩子
            }
            j++;    // 不管能不能吃到饼干，饼干下标都要+1
        }
        return sum;
    }

说明：刚开始做这题的时候，贪心思想是对的，但是我之前经常用for循环，一时间没有想到使用while循环就直接怼for循环了。最开始写的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int findContentChildren(int[] g, int[] s) {
        int sum = 0;
        Arrays.sort(g); // 将g数组即孩子胃口数组从小到大排序
        Arrays.sort(s); // 将s数组即饼干尺寸数组从小到大排序
        for (int i = 0; i < g.length; i++) {
            for (int j = 0; j < s.length; j++) {
                if (s[j]>=g[i]){    // 可以吃饼干
                    sum++;
                    s[j]=0; // 被吃掉的饼干尺寸置为0
                    break;  // 吃完即退出内层循环，开始为下一个孩子找饼干
                }
            }
        }
        return sum;
    }
}

这个代码嵌套了两层循环（其实完全没有必要，用while循环就能搞定），最终运行结果为：解答成功:执行耗时:93 ms,击败了5.02% 的Java用户，内存消耗:39.1 MB,击败了57.48% 的Java用户。然后我将该代码改善成上述代码，结果为：解答成功:执行耗时:7 ms,击败了99.78% 的Java用户，内存消耗:39.2 MB,击败了43.24% 的Java用户。

以后就应该吸取经验，不能一上手就无脑for循环。

495. 提莫攻击

LeetCode 495. 提莫攻击

模拟

这是一道简单的模拟题，只要搞清楚题意，就大致知道思路了。

结合一下代码再画个草图，就可以解出此题了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int findPoisonedDuration(int[] timeSeries, int duration) {
        if (timeSeries.length==1){
            return duration;
        }
        int result = 0;
        for (int i = 0; i < timeSeries.length - 1; i++) {
            if (timeSeries[i+1]-timeSeries[i]<=duration){
                result = result+timeSeries[i+1]-timeSeries[i];
            }else {
                result = result+duration;
            }
        }
        return result + duration;
    }
}

504. 七进制数

LeetCode 504. 七进制数

数学

思路很简单，就是简单的数学运算。以100为例：

代码实现也很简单，注意一下负数的处理即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public String convertToBase7(int num) {
        StringBuilder ans = new StringBuilder();
        if (num<7 && num >-7){
            return String.valueOf(num);
        }
        if (num<0){ // 对负数的处理
            ans.append("-");
            num = -num;
        }
        ArrayDeque<Integer> stack = new ArrayDeque<>();
        // 数学处理
        while (num!=0){
            stack.addLast(num%7);
            num = num/7;
        }
        while (!stack.isEmpty()){
            ans.append(stack.removeLast());
        }
        return ans.toString();
    }
}

521. 最长特殊序列 Ⅰ

LeetCode 521. 最长特殊序列 Ⅰ

脑筋急转弯

这题是一道简单题，一开始我一直在寻找测试用例，试图来寻找规律。但是我发现不管怎么样，只要两个字符串不一样，结果就是两个字符串中长度较长的那个。正当我疑惑时，参考三叶大佬题解发现，原来还真只有这一个规律。

当两字符串不同时，我们总能选择长度最大的字符串作为答案，而当两字符串相同时，我们无法找到特殊序列。

代码如下：

1
2
3
4
5
class Solution {
    public int findLUSlength(String a, String b) {
        return a.equals(b)? -1: Math.max(a.length(),b.length());
    }
}

522. 最长特殊序列 II

LeetCode 522. 最长特殊序列 II

暴力算法

这题我怎么就看不太懂呢。。看了下评论才大致看懂。题解思路大致为：先将数组strs按照字符创长度降序排序，然后依次遍历，如果strs数组中任意一个字符串（除了遍历到的strs[i]）都不是遍历到的当前字符串strs[i]的子序列的话，那么就返回这个字符串strs[i]的长度；如果遍历到最后还没有合法的值，那么就返回-1。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public int findLUSlength(String[] strs) {
        Arrays.sort(strs, (o1, o2) -> o2.length()-o1.length());
        for (int i = 0; i < strs.length; i++) {
            boolean flag=true;
            // strs[j].length()<strs[i].length(),说明strs[j]一定不是strs[i]的子序列
            for (int j = 0; j < strs.length && strs[j].length()>=strs[i].length(); j++) {
                if(j==i) {
                    continue;
                }
                if (isSubSeq(strs[j],strs[i])){ // strs[j]是strs[i]的子序列，更新flag的值
                    flag = false;
                }
            }
            if (flag){      // flag为true才是合法值
                return strs[i].length();
            }
        }
        return -1;
    }

    /**
     * 判断字符串b是否为字符串a的子序列（a.length >= b.length）
     * @return 是子序列返回true；否则返回false
     */
    private boolean isSubSeq(String a, String b) {
        if (b.equals(a)){
            return true;
        }
        // 双指针，i指向a的开头，j指向b开头
        int i = 0;
        int j = 0;
        for (i = 0; i < a.length(); i++) {
            if (a.charAt(i)==b.charAt(j)){  // j继续向下遍历的条件
                j++;
            }
            if (j==b.length()){ // 如果j走遍了字符串b，说明b是a的子序列
                return true;
            }
        }
        return false;
    }
}

其中Arrays.sort(strs, (o1, o2) -> o2.length()-o1.length());是Lambda表达式，其原始形式为：

1
2
3
4
5
6
Arrays.sort(strs, new Comparator<String>() {
    @Override
    public int compare(String o1, String o2) {
       return o2.length()-o1.length();
    }
});
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public int findLUSlength(String[] strs) {
        Arrays.sort(strs, (o1, o2) -> o2.length()-o1.length());
        for (int i = 0; i < strs.length; i++) {
            boolean flag = true;    // 不是子序列，即strs[i]为合法值
            for (int j = i+1; j < strs.length; j++) {
                if (strs[j].length()<strs[i].length()){ // 说明strs[j]一定不是strs[i]的子序列
                    break;
                }
                if (isSubSeq(strs[i],strs[j])){ // strs[j]是strs[i]的子序列，更新flag的值
                    flag = false;
                }
            }
            if (flag){      // flag为true才是合法值
                return strs[i].length();
            }
        }
        return -1;
    }

    /**
     * 判断字符串b是否为字符串a的子序列（a.length >= b.length）
     * @return 是子序列返回true；否则返回false
     */
    private boolean isSubSeq(String a, String b) {
        if (b.equals(a)){
            return true;
        }
        // 双指针，i指向a的开头，j指向b开头
        int i = 0;
        int j = 0;
        for (i = 0; i < a.length(); i++) {
            if (a.charAt(i)==b.charAt(j)){  // j继续向下遍历的条件
                j++;
            }
            if (j==b.length()){ // 如果j走遍了字符串b，说明b是a的子序列
                return true;
            }
        }
        return false;
    }
}

537. 复数乘法

LeetCode 537. 复数乘法

模拟

这题是一道模拟题。我们只需要先将复数的乘法运算模拟一下，就很好求解了。

所以关键只需要求出a1，a2，b1，b2即可。像这种类似在字符串中找出有效item，之前已经实现过了，简单的双指针即可实现。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public String complexNumberMultiply(String num1, String num2) {
        // 读取a1，b1
        int a1=0;
        int b1=0;
        int i = 0;
        int j = 0;
        while (num1.charAt(j)!='+'){
            j++;
        }
        // 读取到a1了
        a1 = Integer.parseInt(num1.substring(i,j));
        i = j+1;
        while (num1.charAt(j)!='i'){
            j++;
        }
        // 读取到b1了
        b1 = Integer.parseInt(num1.substring(i,j));
        // 读取a2，b2
        int a2=0;
        int b2=0;
        i = 0;
        j = 0;
        while (num2.charAt(j)!='+'){
            j++;
        }
        a2 = Integer.parseInt(num2.substring(i,j));
        i = j+1;
        while (num2.charAt(j)!='i'){
            j++;
        }
        b2 = Integer.parseInt(num2.substring(i,j));
        int x = a1*a2-b1*b2;
        int y = a1*b2+a2*b1;
        StringBuilder ans = new StringBuilder();
        ans.append(x).append("+").append(y).append("i");
        return ans.toString();
    }
}

宫水三叶大佬的题解简洁的多，因为使用了Java String类的split方法，按照给定的正则表达式来进行切割。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public String complexNumberMultiply(String num1, String num2) {
        // 直接用Java String类的split方法，按照给定的正则表达式来进行切割
        String[] ss1 = num1.split("\\+|i"), ss2 = num2.split("\\+|i");
        int a = Integer.parseInt(ss1[0]), b = Integer.parseInt(ss1[1]);
        int c = Integer.parseInt(ss2[0]), d = Integer.parseInt(ss2[1]);
        int x = a * c - b * d, y = b * c + a * d;
        StringBuilder ans = new StringBuilder();
        ans.append(x).append("+").append(y).append("i");
        return ans.toString();
    }
}

553. 最优除法

LeetCode 553. 最优除法

模拟

这题，emm只需要简单的数学模拟就可以知道，分子固定是第一个数，分母就是后面的数依次除下去。

分子固定第一个数，分母越小越好，怎样才会越小越好，因为题目限制了数字诠释正整数，肯定越除越小，那就把从第二个数开始到结尾的所有数全部作为分母，这样的时候最小。

虽然是道中等题，但是数学分析之后又觉得太简单了。题目说可以在任意位置添加任意数目的括号，但是经过数学分析后可以知道：只需要添加一个括号即可！

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public String optimalDivision(int[] nums) {
        int length = nums.length;
        StringBuilder ans = new StringBuilder();
        // 首先先将数组中的数以此添加/
        for (int i = 0; i < length; i++) {
            if (i>0){
                ans.append("/");
            }
            ans.append(nums[i]);
        }
        // 接下来添加括号
        if (length>2){  // length>2才需要添加括号
            // 在第一个/后面添加(，在最末尾添加)
            ans.insert(ans.indexOf("/")+1, "(" );
            ans.append(")");
        }
        return ans.toString();
    }
}

564. 寻找最近的回文数

LeetCode 564. 寻找最近的回文数

模拟

官方题解

构造回文整数有一个直观的方法：用原数的较高位的数字替换其对应的较低位。例如，对于数 12345，我们可以用 1 替换 5，用 2 替换 4，这样原数即变为回文整数 12321。

在这种方案中，我们修改的都是较低位的数字，因此构造出的新的整数与原数较为接近。大部分情况下，这种方案是最优解，但还有部分情况我们没有考虑到：

  1. 构造的回文整数大于原数时，我们可以减小该回文整数的中间部分来缩小回文整数和原数的差距。例如，对于数 99321，我们将构造出回文整数 99399，实际上 99299 更接近原数。
    • 当我们减小构造的回文整数时，可能导致回文整数的位数变化。例如，对于数 100，我们将构造出回文整数 101，减小其中间部分将导致位数减少。得到的回文整数形如 999…999999 \ldots 999 ( 10len −110^{\text {len }}-1 )。
  2. 构造的回文整数小于原数时，我们可以增大该回文整数的中间部分来缩小回文整数和原数的差距。例如，对于数 12399，我们将构造出回文整数 12321，实际上 12421 更接近原数。
    • 当我们增大构造的回文整数时，可能导致回文整数的位数变化。例如，对于数 998 ，我们将构 造出回文整数 999 ，增大其中间部分将导致位数增加。得到的回文整数形如 100…001100 \ldots 001 ( 10len+110^{l e n}+1 ）。
  3. 构造的回文整数等于原数时，由于题目约定，我们需要排除该回文整数，在其他的可能情况中寻找最近的回文整数。

考虑到以上所有的可能，我们可以给出最终的方案。分别计算出以下每一种可能的方案对应的回文整数，在其中找到与原数最近且不等于原数的数即为答案：

  1. 用原数的前半部分替换后半部分得到的回文整数
  2. 用原数的前半部分加一后的结果替换后半部分得到的回文整数
  3. 用原数的前半部分减一后的结果替换后半部分得到的回文整数
  4. 为防止位数变化导致构造的回文整数错误，因此直接构造 999…999 和 100…001 作为备选答案（以12399为例，直接构造9999和10001）

举个例子：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public String nearestPalindromic(String n) {
        long number = Long.parseLong(n);
        Long ans = -1L;
        List<Long> candidates = getCandidates(n);   // 获取候选的几个数
        // 找到与原数最近且不等于原数的数即为答案
        for (Long candidate : candidates) {
            if (candidate != number) {
                if (ans == -1) {   // 先给ans赋一个候选值
                    ans = candidate;
                } else if (Math.abs(candidate - number) < Math.abs(ans - number)) {  // 取最近的
                    ans = candidate;
                } else if (Math.abs(candidate - number) == Math.abs(ans - number) && candidate < ans) { // 一样近，取最小的
                    ans = candidate;
                }
            }
        }
        return Long.toString(ans);
    }

        /**
         * 根据我们分析出的条件，返回一个候选结果列表
         * @param n
         * @return
         */
        private List<Long> getCandidates (String n){
            int length = n.length();
            List<Long> list = new ArrayList<>();
            long prefix = Long.parseLong(n.substring(0, (length + 1) / 2));   // 前一半数字(前缀)
            // 前三种情况，即前缀-1，前缀，前缀+1
            for (long i = prefix - 1; i <= prefix + 1; i++) {
                StringBuilder sb = new StringBuilder();
                String prefix_str = String.valueOf(i);  // 前缀
                StringBuilder suffix_str = new StringBuilder(prefix_str).reverse(); // 后缀
                if (length % 2 == 0) { // 注意添加后缀时，不要重复了中间的数字
                    sb.append(prefix_str).append(suffix_str.substring(0));
                } else {
                    sb.append(prefix_str).append(suffix_str.substring(1));
                }
                String candidate = sb.toString();
                list.add(Long.parseLong(candidate));
            }
            // 第四种情况
            list.add((long) Math.pow(10, length - 1) - 1);  // 99...99
            list.add((long) Math.pow(10, length) + 1);    // 100..001
            return list;
        }
}

566. 重塑矩阵

LeetCode 566. 重塑矩阵

数组

思路比较简单，直接看代码吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int[][] matrixReshape(int[][] mat, int r, int c) {
        int m = mat.length;
        int n = mat[0].length;
        if (m*n != r*c){
            return mat;
        }
        int[][] arr = new int[r][c];
        ArrayDeque<Integer> deque = new ArrayDeque<>();
        for (int[] ints : mat) {
            for (int anInt : ints) {
                deque.addLast(anInt);
            }
        }
        for (int i = 0; i < r; i++) {
            for (int j = 0; j < c; j++) {
                arr[i][j] = deque.removeFirst();
            }
        }
        return arr;
    }
}

二维数组的一维表示

官方题解

对于一个行数为 m，列数为 n，行列下标都从 0 开始编号的二维数组，我们可以通过下面的方式，将其中的每个元素 (i, j) 映射到整数域内，并且它们按照行优先的顺序一一对应着 [0, m*n)中的每一个整数。形象化地来说，我们把这个二维数组排扁成了一个一维数组。

这样的映射即为：

(i,j)→i×n+j(i, j) \rightarrow i \times n+j

同样地，我们可以将整数 x 映射回其在矩阵中的下标，即：

{i=x/nj=x%n\left\{\begin{array}{l} i=x / n \\ j=x \% n \end{array}\right.

这个搞清楚了，这题就很好解了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int[][] matrixReshape(int[][] mat, int r, int c) {
        int m = mat.length;
        int n = mat[0].length;
        if (m*n != r*c){
            return mat;
        }
        int[][] arr = new int[r][c];
        for (int x = 0; x < m * n; x++) {
            arr[x/c][x%c] = mat[x/n][x%n];
        }
        return arr;
    }
}

589. N 叉树的前序遍历

LeetCode 589. N 叉树的前序遍历

深度优先搜索（BFS）

跟二叉树的前序遍历类似。前序遍历即根-左-右。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    ArrayList<Integer> list = new ArrayList<>();
    public List<Integer> preorder(Node root) {
        if (root!=null){
            list.add(root.val);
            for (Node node : root.children) {
                preorder(node);
            }
        }
        return list;
    }
}

写的更像dfs一点的话，代码可以如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public List<Integer> preorder(Node root) {
        ArrayList<Integer> list = new ArrayList<>();
        dfs(root,list);
        return list;
    }

    private void dfs(Node node, ArrayList<Integer> list) {
        if (node!=null){
            list.add(node.val);
            for (Node child : node.children) {
                dfs(child,list);
            }
        }
    }
}

590. N 叉树的后序遍历

LeetCode 590. N 叉树的后序遍历

深度优先搜索（BFS）

跟二叉树的后序遍历类似。后序遍历即左-右-根。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    List<Integer> ans = new ArrayList<>();
    public List<Integer> postorder(Node root) {
        dfs(root);
        return ans;
        
    }

    private void dfs(Node node) {
        if (node==null){
            return;
        }
        for (Node child : node.children) {
            dfs(child);
        }
        ans.add(node.val);
    }
}

599. 两个列表的最小索引总和

LeetCode 599. 两个列表的最小索引总和

模拟+哈希表

这是一道简单模拟题。理解题意后使用Hash表就能实现。思路比较清晰看代码就能搞懂。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public String[] findRestaurant(String[] list1, String[] list2) {
        List<String> list = new ArrayList<>();
        int min = Integer.MAX_VALUE;    // 记录后面遍历过程中的最小索引和
        // key存储list1的字符串，value存储该字符串在list1中的索引
        Map<String, Integer> map = new HashMap<>();
        for (int i = 0; i < list1.length; i++) {
            map.put(list1[i], i);
        }
        // 接下来遍历list2
        for (int i = 0; i < list2.length; i++) {
            if (map.containsKey(list2[i])){
                // 判断是否是最小索引和
                if (map.get(list2[i])+i<min){   // 新的最小索引和
                    list.clear();
                    list.add(list2[i]);
                    min = map.get(list2[i])+i;
                }else if (map.get(list2[i])+i==min){
                    list.add(list2[i]);
                }
            }
        }
        String[] ans = new String[list.size()];
        for (int i = 0; i < list.size(); i++) {
            ans[i] = list.get(i);
        }
        return ans;
    }
}

605. 种花问题

LeetCode 605. 种花问题

双指针

这题我用双指针来解决。首先定义result为我们能最多插入的花。分析如下：

  • 首先来看一般情况，中间的两个1之间，如果有x个0，那么最多就可以插入（x-1）/2枝花（简单的数学问题，画下图就能看懂）
  • 接下来来看两个特特殊况：
    • 开头前两个均为0：处理方式为另开头的0为1，result++
    • 倒数两个均为0：处理方式为另倒数第一个的0为1，result++

在对上述两种特殊情况处理完毕后，接下来的问题就是如何计算两个1之间0的值x了，这里我采用了双指针的方法，设置两个指针a，b，初始时分别指向0和1：

  • b每次都向右移动一位，当b移动到1时，计算a和b之间0的个数，很明显可以看出是b-a-1，即x=b-a-1
  • 计算出x后，我们再根据x来求出最多能插入的花的数目，（x-1）/2通过数学合并即为(b-a-2)/2， result = result + (b-a-2)/2;即可
  • result相加后，使a指针指向b的位置：a = b;，然后b再次向右移动重复上述循环，直到b走到了数组的最后一位

最后的最后，别忘了对flowerbed长度为1的处理：

1
2
3
4
5
6
if (flowerbed.length==1){   // flowerbed长度为1
    if (n==0){
        return true;
    }
    return flowerbed[0]==0;
}

计算出result剩下的就很好做了，直接return result>=n;即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public boolean canPlaceFlowers(int[] flowerbed, int n) {
        if (flowerbed.length==1){   // flowerbed长度为1
            if (n==0){
                return true;
            }
            return flowerbed[0]==0;
        }
        int result = 0; // 能插入的最大花数
        if (flowerbed[0]==0&&flowerbed[1]==0){   // 特殊情况之开头前两个均为0
            flowerbed[0]=1;
            result++;
        }
        if (flowerbed[flowerbed.length-1]==0&&flowerbed[flowerbed.length-2]==0){   // 特殊情况之倒数两个均为0
            flowerbed[flowerbed.length-1]=1;
            result++;
        }
        // 定义两个指针a，b，便于计算两个1之间0的个数
        int a = 0;
        int b = 1;
        while (b<flowerbed.length){
            // b指针指到了1，先计算a，b之间0的个数，然后将a指针移动到b指针
            if (flowerbed[b]==1){
                result  = result + (b-a-2)/2;   // 数学合并处理
                a = b;
            }
            b++;
        }
        return result>=n;
    }
}

结果为：解答成功:执行耗时:1 ms,击败了89.55% 的Java用户，内存消耗:39.9 MB,击败了53.91% 的Java用户

贪心算法

上面的双指针的思想，可能还是步骤较多，运行时间为1ms。接下来我们使用贪心算法，我们只需要定义一个指针i=0，就可以直接开始遍历。遍历规则的关键点就一个：1的左右两个都不能插花

在遍历的过程中，贪心思想（遍历规则）如下：

  • 第一种情况：如果第i个元素为1，说明第i和第i+1的位置都不能插花，直接i = i + 2
  • 第二种情况：可以插花，这里需要区分两种情况：
    • i还在数组的中间位置，如果第i个元素和第i+1个元素都为0，说明可以在i处置1，n--，然后i = i+2
    • i已经到了数组的最后一个位置，根据我们的遍历规则（1的左右两个都不能插花），i既然跳转到了最后一个位置，说明i的前一个位置必为0！所以可以插花，n--
  • 第三种情况：不能插花，i指向0而i+1指向1，i = i+3

说的更清楚点，就是（下面的例子中i都指向第一个数字）：

  • 10的情况：不能插花，i = i+2
  • 00的情况：可以插花，n--之后，i = i+2
  • 01的情况：不能插花，i = i+3

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public boolean canPlaceFlowers(int[] flowerbed, int n) {
        if (n==0){  // n为0，直接return true;
            return true;
        }
        for (int i = 0; i < flowerbed.length;) {
            if (flowerbed[i]==1){   // 10的情况
                i = i + 2;
            } else if ((i==flowerbed.length-1)||(i<flowerbed.length-1)&&flowerbed[i+1]==0) {    // 00的情况
                n--;
                if (n==0){  // n到0了就直接return true;
                    return true;
                }
                i = i + 2;
            }else { // 01的情况
                i = i + 3;
            }
        }
        return false;
    }
}

结果为：解答成功:执行耗时:0 ms,击败了100.00% 的Java用户，内存消耗:39.9 MB,击败了50.49% 的Java用户

653. 两数之和 IV - 输入 BST

LeetCode 653. 两数之和 IV - 输入 BST

树的搜索+哈希表

官方题解

二叉搜索树(BST)

二叉搜索树的中序遍历是升序排列的。（所以也可以采用中序遍历+双指针来解决）

使用DFS或BFS遍历数的每个节点，同时结合哈希表即可完成此题。在遍历二叉搜索树时，我们使用HashSet来存储k-node.val；如果下次遇到的节点值存在于HashSet，即返回true。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    Set<Integer> set = new HashSet<>();
    public boolean findTarget(TreeNode root, int k) {
        if (root==null){
            return false;
        }
        if (set.contains(root.val)){
            return true;
        }
        set.add(k- root.val);
        return findTarget(root.left,k) || findTarget(root.right,k);
    }
}

670. 最大交换

LeetCode 670. 最大交换

双指针

这题因为给定数字的范围是 [0, 10^8]。所以数字长度不是特别大，使用双指针再嵌套一个for循环就可以0ms 100%了。

思路很简单，题目要求至多可以交换一次数字中的任意两位，那么为了得到最大数，只需要将数字中的最大数移到最高位即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int maximumSwap(int num) {
        String str = String.valueOf(num);
        char[] arr = str.toCharArray();
        int length = arr.length;
        for (int i = 0; i < length-1; i++) {    // i只需要遍历到倒数第二位即可
            // 首先找到j之后的最大值max的索引
            int max = i+1;
            for (int j = i+1; j < length; j++) {
                max = arr[max]>arr[j]? max:j;
            }
            // 之后判断arr[max]和arr[i]的关系
            if (arr[max]>arr[i]){
                char temp = arr[max];
                arr[max] = arr[i];
                arr[i] = temp;
                break;
            }
        }
        String ans = new String(arr);
        return Integer.parseInt(ans);
    }
}

704. 二分查找

LeetCode 704. 二分查找

二分查找

因为题目所给数组是已经排序好的，所以这就是一个二分查找的典型例子。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int search(int[] nums, int target) {
        int length = nums.length;
        if (length==1){ // 特殊情况处理
            return nums[0]==target? 0:-1;
        }
        int left = 0;
        int right = length-1;
        while (left<right){
            int mid = (left+right)/2;
            if (nums[mid]==target){
                return mid;
            }else if (nums[mid]<target){   // 结果小了
                left = mid+1;   // 更新搜索区间为[mid+1, right]
            }else {   // 结果大了
                right = mid;    // 更新搜索区间为[left, mid]
            }
        }
        return nums[left]==target? left:-1;
    }
}

707. 设计链表

LeetCode 707. 设计链表

单链表

单链表的实现在之前的数据结构学习笔记中就已经写过了。在写代码的过程中只要心里清楚头节点和首元节点的区别即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
class MyLinkedList {
    class ListNode {
        int val;
        ListNode next;
        ListNode() {}
        ListNode(int val) { this.val = val; }
        ListNode(int val, ListNode next) { this.val = val; this.next = next; }
    }

    private ListNode dummyNode = null;

    public MyLinkedList() {
        dummyNode = new ListNode();    // 头结点用于区分首元结点
    }
    
    public int get(int index) {
        ListNode temp = dummyNode.next; // temp节点从首元节点开始
        for (int i = 0; i < index; i++) {
            if (temp==null){
                return -1;
            }
            temp = temp.next;
        }
        if (temp==null){
            return -1;
        }
        return temp.val;
    }
    
    public void addAtHead(int val) {
        ListNode newNode = new ListNode(val);
        newNode.next = dummyNode.next;
        dummyNode.next = newNode;
    }
    
    public void addAtTail(int val) {
        ListNode newNode = new ListNode(val);
        ListNode temp = dummyNode;  // temp从头节点开始
        while (temp.next!=null){    // 循环结束后temp即为链表的最后一个节点
            temp = temp.next;
        }
        temp.next = newNode;
    }
    
    public void addAtIndex(int index, int val) {
        if (index<0){   // 如果index小于0，则在头部插入节点
            addAtHead(val);
            return;
        }
        ListNode newNode = new ListNode(val);
        ListNode temp = dummyNode;  // temp从头节点开始
        // 循环结束后，temp节点为index节点的前一个
        for (int i = 0; i < index; i++) {
            if (temp==null){ // 如果index大于链表长度，则不会插入节点
                return;
            }
            temp = temp.next;
        }
        if (temp==null){ // 如果index大于链表长度，则不会插入节点
            return;
        }
        newNode.next = temp.next;
        temp.next = newNode;
    }
    
    public void deleteAtIndex(int index) {
        ListNode temp = dummyNode;  // temp从头节点开始
        // 循环结束后，temp节点为index节点的前一个
        for (int i = 0; i < index; i++) {
            if (temp==null||temp.next==null){
                break;
            }
            temp = temp.next;
        }
        if (temp==null||temp.next==null){
            return;
        }
        temp.next = temp.next.next;
    }
}

709. 转换成小写字母

LeetCode 709. 转换成小写字母

ASCII码应用

注意清楚如何根据ASCII码转换字母大小写即可。在本题中通过arr[i] = (char) (arr[i]+32);将大写字母转换成小写字母。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public String toLowerCase(String s) {
        char[] arr = s.toCharArray();
        for (int i = 0; i < arr.length; i++) {
            if ('A'<=arr[i] && arr[i]<='Z' ){
                arr[i] = (char) (arr[i]+32);
            }
        }
        return new String(arr);
    }
}

739. 每日温度

LeetCode 739. 每日温度

单调栈

这题是单调栈的典型题目：即求下一个大于 x或者下一个小于 xx这类题目。

我们创建一个单调栈，保证栈中从栈顶到栈底温度是单调递增的。同时，为了方便后续操作，我们在栈中存储的不是温度本身，而是温度在temperatures数组中的索引。

这里我们准备一个arr数组作为返回的结果数组。

遍历temperatures数组，依次将其push到单调栈中，当出现遍历的当前温度current大于栈顶元素top时，执行以下操作：(这种情况即说明pop出的温度在若干天后(current - top)出现了比它高的温度)

  • 需要pop出若干元素，保证栈是单调栈
  • arr[current] = current - top

遍历结束后，还在栈中的元素，即说明这些温度在之后的时间中再也没有出现比它高的温度了，结果为0。当然我们在初始化的时候值已经是0了，所以无需再进行操作。

文字结合以下草稿，应该就比较清晰了：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int length = temperatures.length;
        int[] arr = new int[length];    // 结果数组
        ArrayDeque<Integer> stack = new ArrayDeque<>(); // 单调栈
        stack.addLast(0); // 先将数组的第一个元素push到栈中
        for (int i = 1; i < length; i++) {
            // 保证是单调栈
            while (!stack.isEmpty() && temperatures[i]>temperatures[stack.getLast()]){
                arr[stack.getLast()] = i - stack.getLast();
                stack.removeLast();
            }
            stack.addLast(i);
        }
        return arr;
    }
}

781. 森林中的兔子

LeetCode 781. 森林中的兔子

模拟+贪心

参考宫水三叶大佬题解。

官方题解

首先我们根据题意可得出以下推论：两只相同颜色的兔子看到的其他同色兔子数必然是相同的。其逆反命题为：若两只兔子看到的其他同色兔子数不同，那么这两只兔子颜色也不同。

提取结论如下：

  • 同一颜色的兔子回答的数值必然是一样的
  • 但回答同样数值的，不一定就是同颜色兔子

设有某种颜色的兔子 m 只，它们回答的答案数值为 cnt，显然有： m=cnt+1。

但如果是在 answers数组里，回答 cnt 的数量为 t 的话呢？这时候我们需要分情况讨论：

  • t<=cnt+1 : 为达到最少的兔子数量，我们可以假定这t只兔子为同一颜色，这样能够满足题意，同时不会导致额外兔子数量增加（同一颜色的兔子回答的数值必然是一样的）
  • t>cnt+1 : 我们知道回答 cnt 的兔子应该有 cnt+1 只。这时候说明有数量相同的不同颜色的兔子回答了同样的数值。为达到最少的兔子数量，我们应当将 t 分为若干种颜色，并尽可能让某一种颜色的兔子为 cnt+1 只，这样能够满足题意，同时不会导致额外兔子数量增加（但回答同样数值的，不一定就是同颜色兔子）。

贪心思想的核心在于：我们应该让同一颜色的兔子数量尽量多，从而实现总的兔子数量最少。

通过数学处理，我们可以得到以下结论：一般地，如果有 x 只兔子都回答 y，则至少有⌈xy+1⌉\left\lceil\frac{x}{y+1}\right\rceil种不同的颜色，且每种颜色有 y+1只兔子，因此兔子数至少为：

⌈xy+1⌉⋅(y+1)\left\lceil\frac{x}{y+1}\right\rceil \cdot(y+1)

有了这个结论，接下来就很好做了。我们可以用HashMap来存储，其中key为回答的结果y，valeu为回答为y的兔子数量x。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int numRabbits(int[] answers) {
        int result = 0;
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int answer : answers) {
            if (map.containsKey(answer)) {
                map.put(answer, map.get(answer) + 1);
            } else {
                map.put(answer, 1);
            }
        }
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
            // x/(y+1)的结果向上取整，可以写成(x+y)/(y+1)向下取整
            int x = entry.getValue();
            int y = entry.getKey();
            result = result + ((x + y)/(y +1))*(y +1);
        }
        return result;
    }
}

注意：在代码上，x/(y+1)的结果向上取整，可以写成(x+y)/(y+1)向下取整！

876. 链表的中间结点

LeetCode 876. 链表的中间结点

单链表

求链表的中间结点，在之前数据结构的学习笔记中就已经实现过了。

这里再简单说一下思路：在未知链表长度的情况下，要找出链表的中间节点，可以设置两个指针p1，p2，都从首元节点开始， p1节点走一步，p2节点走两步，当p2节点为终点时，p1为中间节点。

注意事项：

  • 我们的条件设置为p2!=null && p2.next!=null && p2.next.next!=null
  • 当节点数为奇数时，p2能够走到最后一个节点，此时p1为链表的中间节点
  • 当节点数为偶数时，p2只能走到倒数第2个节点，所以p1为链表中间偏左的节点

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public ListNode middleNode(ListNode head) {
        // 设置两个指针p1，p2
        ListNode p1 = head;
        ListNode p2 = head;
        while (p2!=null&&p2.next!=null&&p2.next.next!=null){
            // p1走一步，p2走两步
            p1 = p1.next;
            p2 = p2.next.next;
        }
        if (p2.next==null){ // 说明p2走到了链表的最后一个节点，链表长度为奇数
            return p1;
        }
        return p1.next; // 节点数为偶数，p1为链表中间偏左的节点，而题目要返回中间偏右的节点
    }
}

917. 仅仅反转字母

栈+顺序表

这题我刚开始的思路就是：遍历字符串s，用栈来存储字母方便反转，用顺序表来存储非字母方便后续插入。

意思很好理解，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public String reverseOnlyLetters(String s) {
        StringBuilder ans = new StringBuilder();
        Deque<Character> stack = new ArrayDeque<>();    // 栈，来反转字母
        ArrayList<Integer> list = new ArrayList<>();    // 存储字符串中非字母字符所在的索引
        char[] s_arr = s.toCharArray();
        for (int i = 0; i < s_arr.length; i++) {
            if ((s_arr[i]>='A'&&s_arr[i]<='Z') || (s_arr[i]>='a'&&s_arr[i]<='z') ){ // 字母
                stack.push(s_arr[i]);
            }else {     // 非字母
                list.add(i);
            }
        }
        // 首先将字母反转
        while (!stack.isEmpty()){
            ans.append(stack.pop());
        }
        // 然后插入非字母的字符
        for (Integer index : list) {
            ans.insert(index, String.valueOf(s_arr[index]));
        }
        return ans.toString();
    }
}

结果为：解答成功:执行耗时:2 ms,击败了9.63% 的Java用户，内存消耗:39.7 MB,击败了5.02% 的Java用户。

双指针+模拟

上面的方法效率还是太低了，这里参考一下宫水三叶大佬的题解。

反转典型的双指针，我们分别在字符串开头和末尾定义两个指针，然后分别向中间移动，若遇到了非字母，则该指针继续移动即可。（思路很清晰打下草稿就能搞懂）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public String reverseOnlyLetters(String s) {
        int length = s.length();
        char[] arr = s.toCharArray();
        int l = 0;
        int r = length-1;
        while (l<r){
            if (!Character.isLetter(arr[l])){
                l++;
                continue;
            }
            if (!Character.isLetter(arr[r])){
                r--;
                continue;
            }
            char temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;
            l++;
            r--;
        }
        return String.valueOf(arr);
    }
}

结果为：解答成功:执行耗时:0 ms,击败了100.00% 的Java用户，内存消耗:39.2 MB,击败了18.96% 的Java用户

复杂度分析：

  • 时间复杂度：O(n)
  • 空间复杂度：调用 toCharArray 和构造新字符串均需要与字符串长度等同的空间。复杂度为 O(n)

932. 漂亮数组

LeetCode 932. 漂亮数组

1081. 不同字符的最小子序列

LeetCode 1081. 不同字符的最小子序列

注意：该题与316. 去除重复字母

单调栈

官方题解（含视频）

这题感觉如果没有正确的方向的话是挺难的。官方提供的题解已经说的很好了，这里我用自己的语言分析一下。

要解决这个问题，需要用到：

  • 一个单调栈：为什么要用单调栈呢，因为要保证栈中的结果永远都是字典序最小
  • 两个数组：lastIndex数组存储字符串s中各个字母出现的最后一个位置，visited数组存储各个字符是否已经存在于栈中

接下来就可以遍历字符串s，分析一下单调栈的存储过程：

  • 首先，先判断当前字符是否已经存在于栈中，如果已经存在，什么都不做开始遍历下一个字符（continue）

  • 如果该字符不存在与栈中（这里用while）：

    • 那么就先判断遍历的字符是否大于栈顶元素top，如果遍历的字符大于栈顶字符top，那么就无需执行下面的操作，直接跳出while循环

    • 如果字符小于栈顶元素top，那么就先判断栈的栈顶元素top是否还会再次出现（i<lastIndex[top-'a']），如果top字符在字符串s后面的遍历中还会出现的话，那么就pop出该栈顶元素，同时在visited数组中设置该字符不存在于栈中（visited[top-'a']=false）

      。接着继续拿遍历的字符跟新的栈顶元素进行上述比较（同样要先判断遍历的字符是否大于栈顶元素top，再判断栈的栈顶元素top是否还会再次出现）（这么做是为了保证栈中的结果永远都是字典序最小，所以要用while）

    • while循环结束后，将该字符push到栈中，同时在visited数组中设置该字符已经存在于栈中

      （visited[charArray[i]-'a']=true）

  • 字符串s遍历之后，栈中从栈底到栈顶的顺序即为我们的结果

光看文字描述可能很迷糊，但光看代码也会很迷糊，文字结合代码一起看应该就比较清晰了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public String removeDuplicateLetters(String s) {
        int length = s.length();
        char[] charArray = s.toCharArray();
        // 一个单调栈，两个数组
        ArrayDeque<Character> stack = new ArrayDeque<>();
        // 题目已经说了都是小写，所以长度为26
        int[] lastIndex = new int[26];  // 存储字符串中字母出现的最后一个位置
        boolean[] visited = new boolean[26];    // 存储a-z这26个字母是否已经存在于栈中
        // 这个循环结束后，lastIndex数组即成功存储到a-z(0-25)的字母在字符串s中出现的最后位置
        for (int i = 0; i < length; i++) {
            lastIndex[charArray[i]-'a']=i;
        }
        // 准备工作都已完毕，接下来就可以开始遍历字符串s了
        for (int i = 0; i < length; i++) {
            if (visited[charArray[i]-'a']){ // 字母已经存在与栈中，直接continue
                continue;
            }
            // 注意while循环中还要加上stack不为空
            while (!stack.isEmpty() && charArray[i]<stack.peekLast() && i<lastIndex[stack.peekLast()-'a']){
                Character top = stack.removeLast();
                visited[top-'a'] = false;
            }
            stack.addLast(charArray[i]);
            visited[charArray[i]-'a'] = true;
        }
        // 遍历结束后，栈中结果即字典序最小
        // 因为我们使用ArrayDeque来模拟栈，所以当然可以直接遍历ArrayDeque
        StringBuilder stringBuilder = new StringBuilder();
        for (Character character : stack) {
            stringBuilder.append(character);
        }
        return stringBuilder.toString();
    }
}
  • 时间复杂度：O(n)，n为字符串s的长度
  • 空间复杂度：O(n)，栈的最大深度

1189. “气球” 的最大数量

LeetCode 1189. “气球” 的最大数量

模拟

这是一道模拟的简单题，只要读懂题意就很容易写出来。

首先定义一个长度为5的int数组words，因为单词balloon的单词种类有5种。然后读取text字符串中这五种单词的个数，注意一个balloon单词需要2个l和2个o即可。最后取words数组中的最小值即为最终结果。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int maxNumberOfBalloons(String text) {
        char[] array = text.toCharArray();
        int[] words = new int[5];
        for (char c : array) {
            if (c == 'a') {
                words[0]++;
            } else if (c == 'b') {
                words[1]++;
            } else if (c == 'l') {
                words[2]++;
            } else if (c == 'n') {
                words[3]++;
            } else if (c == 'o') {
                words[4]++;
            }
        }
        // 一个balloon单词需要2个l和2个o
        words[2] = words[2]/2;
        words[4] = words[4]/2;
        int res = words[0];
        for (int count : words) {
            res = Math.min(res,count);
        }
        return res;
    }
}

1601. 最多可达成的换楼请求数目

LeetCode 1601. 最多可达成的换楼请求数目

二进制枚举

参考宫水三叶大佬的题解。

为了方便，我们令数组 requests的长度为 m。数据范围很小，n的范围为 20，而 m的范围为 16。

根据每个 requests[i] 是否选择与否，共有 2^m种状态（不超过 70000种状态）。我们可以采用二进制枚举的思路来求解，使用二进制数 state 来表示对 requests[i]的选择情况，当 state 的第 k 位为 1，代表 requests[k] 被选择。

我们枚举所有的 state 并进行合法性检查，从中选择出包含请求数的最多（二进制表示中包含 1 个数最多）的合法 state，其包含的请求数量即是答案。

其中统计state中1的个数可以使用 lowbit，复杂度为 O(m)，判断合法性则直接模拟即可（统计每座建筑的进出数量，最后判定进出数不相等的建筑数量是为 0），复杂度为 O(m)，整体计算量为不超过 2*10^6，可以过。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    int[][] rs; // 定义全局变量，方便后续生成的两个函数对requests的引用
    public int maximumRequests(int n, int[][] requests) {
        int ans = 0;
        rs = requests;
        int m = rs.length;  // m个请求
        // 二进制枚举，需要一个m位的二进制数
        for (int i = 0; i < (1 << m); i++) {
            int current = getCurrent(i);
            if (ans>current){   // 没有比ans大，无需判断合法性
                continue;
            }
            if (check(i)){  // 判断合法性
                ans = current;
            }
        }
        return ans;
    }

    /**
     * 合法性判断
     * @param num 十进制要转成二进制，其中第k位为1，代表requests[k]被选择
     * @return 合法返回true
     */
    private boolean check(int num) {
        int[] arr = new int[20];    // 最多20栋楼
        for (int i = 0; i < 16; i++) {  // 根据题意，num转二进制最多16位（最多16个请求）
            if (((num>>i)&1) == 1){   // 位运算。其实就是第i位是1
                int from = rs[i][0];
                int to = rs[i][1];
                arr[from]--;
                arr[to]++;
            }
        }
        for (int i : arr) {
            if (i!=0){  // 只要有一个不为0，就要返回false
                return false;
            }
        }
        return true;
    }

    /**
     * 返回一个十进制数转换成二进制数后，其中1的个数
     * @param num 给定的十进制数
     * @return 返回该十进制数转换成二进制数后，其中1的个数
     */
    private int getCurrent(int num) {
        int count = 0;
        for (int i = num; i != 0; i = i-(i&-i)) {
            count++;
        }
        return count;
    }
}

复杂度分析：

  • 时间复杂度：令 m 为 requests 长度，共有 2^m种选择状态，计算每个状态的所包含的问题数量复杂度为 O(m)，计算某个状态是否合法复杂度为 O(m)；整体复杂度为 O(2^m * m)。
  • 空间复杂度：O(n)

这题进行了大量的位运算，对于对应代码再进行一些解释：

左移运算<<和右移运算>>就不多说了。（Java 运算符）

首先是getCurrent方法。它的作用就是返回一个十进制数num，转换为二进制数后二进制中1的个数。在实现时，用到了lowbit 运算。具体体现在：

1
2
3
for (int i = num; i != 0; i = i-(i&-i)) {
    count++;
}

lowbit还有另一种写法：

1
2
3
for (int i = num; i != 0; i = i&(i-1)) {
    count++;
}

【位运算】深入理解并证明 lowbit 运算

接下来是check方法。这是我们用来判断合法性的方法。其中if (((num>>i)&1) == 1)的意思其实就是二进制数中第i位为1。

check方法的实现逻辑，可以画个草图如下：

1705. 吃苹果的最大数目

LeetCode 1705. 吃苹果的最大数目

小根堆+贪心

这题根据题目意思，很容易就知道可以使用小根堆+算法来解决。我们向小根堆里存苹果最早腐败的天数，即i+days[i]。贪心思想就是：每次都poll出i+days[i]最小的苹果，这样就可以保证能吃到最多的苹果。

因为0 <= apples[i], days[i] <= 2 * 104，所以我们不可能将苹果一个一个的add到小根堆中。这里我的处理是新建一个Apple类，其中有两个成员变量：date和count，分别表示第date天就不能吃了和苹果的数量。然后让其实现Comparable接口，是Apple类按照date的值进行升序排序。Apple类代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Apple implements Comparable<Apple>{
    public int date;   // 第date天开始就不能吃了，即date=i + days[i]
    public int count;  // 苹果的数量

    public Apple(int date, int count) {
        this.date = date;
        this.count = count;
    }

    @Override
    public int compareTo(Apple o) {
        return this.date - o.date;  // 根据apple的date进行升序排列（自然排列）
    }
}

接下来的逻辑就比较好理解了，poll一个apple对象，比较其date和i的关系，若poll.date>i，则说明可以吃这个苹果；n天结束后还要继续进行while循环，直到小根堆为空。这里的逻辑非常好理解，稍微打下草稿就能搞懂。

这里就直接给出代码了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
    class Apple implements Comparable<Apple>{
        public int date;   // 第date天开始就不能吃了，即date=i + days[i]
        public int count;  // 苹果的数量

        public Apple(int date, int count) {
            this.date = date;
            this.count = count;
        }

        @Override
        public int compareTo(Apple o) {
            return this.date - o.date;  // 根据apple的date进行升序排列（自然排列）
        }
    }

    public int eatenApples(int[] apples, int[] days) {
        int n = apples.length;
        int ans = 0;
        // 已经重写Apple类的compareTo方法了，优先队列会根据apple的date进行升序排列
        PriorityQueue<Apple> priorityQueue = new PriorityQueue<>();
        // 第一个for循环，是n天之前的
        for (int i = 0; i < n; i++) {
            if (apples[i]>0){   // apples[i]=0，没有必要将其add到小根堆中
                priorityQueue.add(new Apple(i+days[i],apples[i]));
            }
            // 开始吃苹果
            while (!priorityQueue.isEmpty()){
                Apple poll = priorityQueue.poll();
                if (poll.date>i){    // 可以吃
                    ans++;
                    // 吃完苹果count--，如果不为0还要add到小根堆中
                    poll.count--;
                    if (poll.count>0){
                        priorityQueue.add(poll);
                    }
                    break;  // 一天只能吃一个，吃了就退出while循环
                }
            }
        }
        // for循环结束后，在这n天之后可以继续吃苹果
        int day = n;
        while (!priorityQueue.isEmpty()){
            Apple poll = priorityQueue.poll();
            if (poll.date>day){    // 可以吃
                ans++;
                // 吃完苹果count--，如果不为0还要add到小根堆中
                poll.count--;
                if (poll.count>0){
                    priorityQueue.add(poll);
                }
                day++;  // 一天只能吃一个，吃完就day++
            }
        }
        return ans;
    }
}
  • 时间复杂度：n为数组长度，最多有n组苹果入堆/出堆。复杂度为O(nlogn)（因为小根堆的add和poll操作时间复杂度均为O(log n)）
  • 空间复杂度：O(n)

宫水三叶大佬在这题中的解决思路跟我差不多，但是在代码上是直接往小根堆中存储二维数组的。

大佬代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int eatenApples(int[] apples, int[] days) {
        PriorityQueue<int[]> q = new PriorityQueue<>((a,b)->a[0]-b[0]);
        int n = apples.length, time = 0, ans = 0;
        while (time < n || !q.isEmpty()) {
            if (time < n && apples[time] > 0) q.add(new int[]{time + days[time] - 1, apples[time]});
            while (!q.isEmpty() && q.peek()[0] < time) q.poll();
            if (!q.isEmpty()) {
                int[] cur = q.poll();
                if (--cur[1] > 0 && cur[0] > time) q.add(cur);
                ans++;
            }
            time++;
        }
        return ans;
    }
}

1706. 球会落何处

LeetCode 1706. 球会落何处

模拟

参考宫水三叶大佬题解

本题的关键是要通过模拟将小球的运动在代码上体现出来，即要记录小球坐标的变化。

我们使用 r 和 c 表示小球当前所处的位置，受重力影响，在不被卡住的情况下，r 会持续自增，直到到达底部；而 c 的变化，则是取决于当前挡板 grid[r][c] 的方向：

  • 若 grid[r][c] 为 1，则小球的下一个位置为(r+1,c+1)；
  • 若 grid[r][c] 为−1，则下一位置为(r+1,c−1)。

即可以统一表示为(r+1,c+grid[r][c])。

当且仅当小球在本次移动过程中没被卡住，才能继续移动。没有被卡住的情况有：

  • c+grid[r][c] 没有超过矩阵的左右边界（没有被边界卡住）；
  • 并且 grid[r][c] 和 grid[r][c+grid[r][c]] 同向（不形成夹角）。

将以上信息理清楚了，代码就很好写了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    //  m*n的二维网格grid
    int m;
    int n;
    public int[] findBall(int[][] grid) {
        //  m*n的二维网格grid
        m = grid.length;
        n = grid[0].length;
        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {   // 开始遍历每个小球
            ans[i] = getValue(i, grid);
        }
        return ans;
    }

    /**
     * 计算小球落下的位置
     * @param x 小球初始所在位置
     * @param grid 题目所给的二维网格
     * @return 小球不能落下则返回-1
     */
    private int getValue(int x, int[][] grid) {
        int r = 0;
        int c = x;
        while (r<m){    // r<m,则说明小球还没有落地
            int next = c+grid[r][c];    // 小球下一个到的横坐标位置
            if (next<0 || next > n-1){    // 超过网格边界，被网格卡住（注意是next > n-1）
                return -1;
            }
            if (grid[r][c]!=grid[r][next]){ // 楼梯不同向，被卡住
                return -1;
            }
            // 没有被卡住的情况,更新小球的坐标即可
            r++;
            c = next;
        }
        // 能够跑完完整的while循环，说明小球落地了
        return c;
    }
}

复杂度分析：

  • 时间复杂度：O(m*n)
  • 空间复杂度：O(n)

1725. 可以形成最大正方形的矩形数目

LeetCode 1725. 可以形成最大正方形的矩形数目

模拟

这是一道简单模拟题，只要读懂题意就很容易写出题解。

我们只需要先求出各个矩形中能得出的最大正方形边长，将其存放于于side数组中，最后求出side数组中最大值的个数即为结果。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int countGoodRectangles(int[][] rectangles) {
        int[] side = new int[rectangles.length];
        for (int i = 0; i < rectangles.length; i++) {
            side[i] = Math.min(rectangles[i][0], rectangles[i][1]);
        }
        Arrays.sort(side);
        int result = 1;
        for (int i = side.length - 2; i >= 0; i--) {
            if (side[i]!=side[side.length-1]){
                break;
            }
            result++;
        }
        return result;
    }
}

其实代码可以写的更优雅一点，根据三叶大佬的题解，可以得出代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int countGoodRectangles(int[][] rectangles) {
        int max = 0;
        int result = 0;
        int current = 0;
        for (int[] rectangle : rectangles) {
            current = Math.min(rectangle[0], rectangle[1]);
            if (current==max){  // 当前边长为最大值，结果+1
                result++;
            }
            if (current>max){   // 出现了新的最大值，result归1
                max = current;
                result = 1;
            }
        }
        return result;
    }
}

省去了上面对side数组排序的过程（Arrays.sort(side);）

1996. 游戏中弱角色的数量

LeetCode 1996. 游戏中弱角色的数量

排序

官方题解

在读懂题意后，可以巧妙地进行排序，然后就可以一次for循环解决问题了。

我们自定义的排序规则为：

  • 攻击力atk降序排序；
  • atk相等的看作同一组，在atk相等的情况下，即同一组内，按def升序排序。

以下是我当时简单画的草稿，主要稍微理解题意，打下草稿，就能看懂题解代码了。

由于我们在同一组内，def按升序排序，所以只要出现property[1]<maxDefense的情况，一定是遍历到下一组了；而由于atk按降序排序，下一组的atk一定小于上一组，所以此时遍历到的即为弱角色。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int numberOfWeakCharacters(int[][] properties) {
        int result = 0;
        Arrays.sort(properties, (o1, o2) -> {
            if (o1[0]!=o2[0]){  // 攻击力不一样，按攻击力降序排序
                return o2[0]-o1[0];
            }else { // 攻击力一样，按防御力升序排序
                return o1[1]-o2[1];
            }
        });
        int maxDefense = properties[0][1];
        for (int[] property : properties) {
            if (property[1]<maxDefense){    // 同一个组内，def降序，所以出现这种情况说明一定遍历到下一组了
                result++;
            }else {
                maxDefense = property[1];
            }
        }
        return result;
    }
}

复杂度分析：

  • 时间复杂度：O(nlogn)，其中 n为数组的长度。排序的时间复杂度为 O(nlogn)，遍历数组的时间为 O(n)，总的时间复杂度为O(nlogn+n)=O(nlogn)。
  • 空间复杂度：O(logn)，其中 n为数组的长度。排序时使用的栈空间为O(logn)。

注意一下上述代码的Lambda表达式，其原始形式为：

1
2
3
4
5
6
7
8
9
10
Arrays.sort(properties, new Comparator<int[]>() {
    @Override
    public int compare(int[] o1, int[] o2) {
        if (o1[0]!=o2[0]){  // 攻击力不一样，按攻击力降序排序
            return o2[0]-o1[0];
        }else { // 攻击力一样，按防御力升序排序
            return o1[1]-o2[1];
        }
    }
});

2000. 反转单词前缀

LeetCode 2000. 反转单词前缀

模拟+双指针

这是一道模拟简单题，读懂题意差不多就可以解出来了。首先要找到字符ch所在的索引index，其次稍微麻烦一点的就是要逆转0到index的字符串，这里使用双指针来完成。双指针部分代码如下：

1
2
3
4
5
6
7
8
9
10
// 然后利用双指针反转从0到index的字符
int l = 0;
int r = index;
while (l<r){
    char temp = chars[l];
    chars[l] = chars[r];
    chars[r] = temp;
    l++;
    r--;
}

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public String reversePrefix(String word, char ch) {
        char[] chars = word.toCharArray();
        int index = 0;
        // 首先找到ch的索引
        for (int i = 0; i < chars.length; i++) {
            if (chars[i]==ch){
                index = i;
                break;
            }
        }
        // 然后利用双指针反转从0到index的字符
        int l = 0;
        int r = index;
        while (l<r){
            char temp = chars[l];
            chars[l] = chars[r];
            chars[r] = temp;
            l++;
            r--;
        }
        return String.valueOf(chars);   // 字符数组转字符串
    }
}

2016. 增量元素之间的最大差值

LeetCode 2016. 增量元素之间的最大差值

暴力算法

根据题意，套一个双循环依次遍历即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int maximumDifference(int[] nums) {
        int ans = -1;
        for (int i = 0; i < nums.length; i++) {
            for (int j = i+1; j < nums.length; j++) {
                if (nums[i]<nums[j]){
                    ans = Math.max(ans, nums[j]-nums[i]);
                }
            }
        }
        return ans;
    }
}

贪心算法

官方题解

上面的暴力算法，套了两层for循环，时间复杂度为O(n^2)。但是其实i指针没有必要依次遍历每个数组。

贪心思想：当我们固定 j 时，选择的下标 i 一定是满足0<=i<j<n 并且 nums[i] 最小的那个 i。

所以我们要记录一下前缀最小值min，在遍历i的时候，有以下两种情况：

  • nums[i]>min：更新ans为Math.max(ans, nums[i]-min);
  • nums[i]<=min：更新min为nums[i]

举个例子：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int maximumDifference(int[] nums) {
        int ans = -1;
        int min = nums[0];
        for (int i = 1; i < nums.length; i++) {
            if (nums[i]>min){
                ans = Math.max(ans, nums[i]-min);
            }else {
                min = nums[i];
            }
        }
        return ans;
    }
}

2100. 适合打劫银行的日子

LeetCode 2100. 适合打劫银行的日子

暴力算法（TLE）

最开始写的暴力算法代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    public List<Integer> goodDaysToRobBank(int[] security, int time) {
        List<Integer> res = new ArrayList<>();
        int length = security.length;
        for (int i = time; i<=length-1-time; i++) {
            if (check(i,security,time)){    // 检测合法性
                res.add(i);
            }
        }
        return res;

    }

    /**
     * 根据题意检测index的合法性
     * @param i
     * @param security
     * @param time
     * @return
     */
    private boolean check(int i, int[] security, int time) {
        // 向左检测i的合法性
        int l = i-time;
        while (l<i){
            if (security[l]<security[l+1]){
                return false;
            }
            l++;
        }
        // 向右检测i的合法性
        int r = i;
        while (r<i+time){
            if (security[r]>security[r+1]){
                return false;
            }
            r++;
        }
        return true;
    }
}

但是会报Time Limit Exceeded。

前缀和

参考三叶大佬题解。

2104. 子数组范围和

LeetCode 2104. 子数组范围和

暴力算法

暴力算法思路很清晰，就是遍历每一个区间（每一个子数组），记录当前子区间的最大值max和最小值min即可。直接看代码就明白了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public long subArrayRanges(int[] nums) {
        long res = 0;
        for (int i = 0; i < nums.length; i++) {
            int max = nums[i];
            int min = nums[i];
            for (int j = i+1; j < nums.length; j++) {   // 因为子数组只有一个的话范围为0，所以j可以从i+1开始
                max = Math.max(max, nums[j]);
                min = Math.min(min, nums[j]);
                res = res + (max-min);
            }
        }
        return res;
    }
}

单调栈（O(N)）

参考宫水三叶大佬题解。

在上述暴力算法的基础上，我们进行如下思考：

假设有 m 个区间，最终的表达式为 m 个 max−min 之和。

若某个 nums[i] ，在 k1k_{1} 个区间中充当最大值，在 k2k_{2} 个区间中充当最小值，则在最终等式中以 max的形式出现 k1k_{1} 次，在最终等式中以 min形式出现 k2k_{2} 次。

因此我们可以统计每个 nums[i] 成为区间最大值的次数 k1k_{1} 和成为区间最小值的次数 k2k_{2} ， ( k1k_{1}-k2k_{2} ) *nums[i]即为 nums[i] 对于最终答案的贡献。

这样就把问题转换为统计每一个nums[i]成为区间最大值的次数 k1k_{1} 和成为区间最小值的次数 k2k_{2} 了。

考虑如何统计每个 nums[i] 成为区间最值的次数：

  • nums[i] 作为区间最大值的次数：找到 nums[i]n u m s[i] 左右最近一个大于 nums[i]n u m s[i]的位置， 记其为 ll 和 rr 。此时区间左端点共有 i−li-l 个选择，区间右端点共有 r−ir-i 个选择，根据乘法原理， 区间个数为 (i−l)∗(r−i)(i-l) *(r-i) 个；
  • nums[i] 作为区间最小值的次数：同理，找到 nums [i][i] 左右最近一个小于 nums[i]n u m s[i]的 位置，记其为 ll 和 rr ，区间个数为 (i−l)∗(r−i)(i-l) *(r-i) 个。

以上两种，如果走到尽头还没有找到符合条件的，那么就继续再走一步结束。即:

  • 向左没有找到最近一个满足xxx的值，记为-1
  • 向右没有找到最近一个满足xxx的值，记为length

看起来可能比较麻烦，但是画个草图就很容易搞懂了：

即问题切换为：使用单调栈找到某个nums[i]的左边/右边的最近一个符合某种性质的位置，从而知道 nums[i]作为区间最值时，左右端点的可选择个数，再结合乘法原理知道nums[i]能够作为区间最值的区间个数，从而知道nums[i]对答案的贡献。

值得注意的是，由于 nums[i] 存在相同元素，因此上述两边均取等号的做法会导致某些区间被重复计算，因此我们可以**令最近右端点的部分不取等号，确保区间统计不重不漏。**

举个例子：

代码体现在：

  • 我们在统计nums[i]时，记录向左能扩展的距离：单调栈满足条件如下：nums[stack.peekLast()]>=nums[i]

  • 我们在统计nums[i]时，记录向右能扩展的距离：单调栈满足条件如下：nums[stack.peekLast()]>nums[i]

    （以上两种都以nums[i]作为min为例）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    int length;
    public long subArrayRanges(int[] nums) {
        length = nums.length;
        long res = 0;
        // min[i]为nums[i]作为区间最小值的次数；max[i]为nums[i]作为区间最大值的次数
        long[] min = getCnt(nums, true);
        long[] max = getCnt(nums, false);
        for (int i = 0; i < length; i++) {
            res = res + (max[i]-min[i])*nums[i];
        }
        return res;
    }

    /**
     * 给定一个nums[]数组，返回一个min[]数组或max[]数组（单调栈实现）
     * @param nums 给定nums数组
     * @param flag flag为true返回min[]数组；为false返回max[]数组
     * @return
     */
    private long[] getCnt(int[] nums, boolean flag) {
        int[] a = new int[length];  // 向左最近一个……
        int[] b = new int[length];  // 向右最近一个……
        Deque<Integer> stack = new ArrayDeque<>();  // 因为单调栈要求的是最近一个xxx的索引，所以存储的也是索引
        for (int i = 0; i < length; i++) {
            // 这里用三元表达式，根据flag的不同来决定是返回min[]还是max[]
            while (!stack.isEmpty() && (flag? nums[stack.peekLast()]>=nums[i]:nums[stack.peekLast()]<=nums[i])){
                stack.removeLast();
            }
            a[i] = stack.isEmpty()? -1:stack.peekLast();
            stack.addLast(i);
        }
        stack.clear();
        for (int i = length-1; i >= 0; i--) {
            while (!stack.isEmpty() && (flag? nums[stack.peekLast()]>nums[i]:nums[stack.peekLast()]<nums[i])){
                stack.removeLast();
            }
            b[i] = stack.isEmpty()? length: stack.peekLast();
            stack.addLast(i);
        }
        long[] ans = new long[length];
        for (int i = 0; i < length; i++) {
            ans[i] = (long) (i-a[i])*(b[i]-i);
        }
        return ans;
    }
}

复杂度分析：

  • 时间复杂度：O(n)，其中 n 为数组的大小。使用单调栈预处理出四个数组需要 O(n)，计算最大值之和与最小值之和需要 O(n)。
  • 空间复杂度：O(n)。保存四个数组需要 O(n)；单调栈最多保存 n 个元素，需要 O(n))。

关于单调栈的具体实现画一下草图就能搞懂，这里就不再画一遍了。