Java数据结构之堆(优先队列)、散列(哈希表)和并查集
关于这三种的数据结构的代码实现还没写,后面再补。
堆(优先队列)
堆的分类
堆是一棵树,其每个节点都有一个键值,且每个节点的键值都大于等于(或小于等于)其父亲的键值。
每个节点的键值都大于等于其父亲键值的堆叫做小根堆,否则叫做大根堆。
- 大根堆:大根堆就是无论在任何一棵(子)树中,父节点都是最大的
- 小根堆:小根堆就是无论在任何一棵(子)树中,父节点都是最小的

习惯上,不加限定提到“堆”时往往都指二叉堆。
堆和普通树的区别
堆并不能取代二叉搜索树,它们之间有相似之处也有一些不同。我们来看一下两者的主要差别:
- **节点的顺序。**在二叉搜索树中,左子节点必须比父节点小,右子节点必须必比父节点大。但是在堆中并非如此。在最大堆中两个子节点都必须比父节点小,而在最小堆中,它们都必须比父节点大。
- **内存占用。**普通树占用的内存空间比它们存储的数据要多。你必须为节点对象以及左/右子节点指针分配内存。堆仅仅使用一个数据来存储数组,且不使用指针。
- 平衡。二叉搜索树必须是“平衡”的情况下,其大部分操作的复杂度才能达到O(log n)。你可以按任意顺序位置插入/删除数据,或者使用 AVL 树或者红黑树,但是在堆中实际上不需要整棵树都是有序的。我们只需要满足堆属性即可,所以在堆中平衡不是问题。因为堆中数据的组织方式可以保证O(log n) 的性能。
- **搜索。**在二叉树中搜索会很快,但是在堆中搜索会很慢。在堆中搜索不是第一优先级,因为使用堆的目的是将最大(或者最小)的节点放在最前面,从而快速的进行相关插入、删除操作。
二叉堆
二叉堆的结构一棵完全二叉树,每个结点中存有一个元素(或者说,有个权值)。
在之前哈夫曼树的笔记中,我们就用代码实现了小根堆。
用数组实现二叉堆
完全可以用数组来实现二叉堆。用数组来实现树相关的数据结构也许看起来有点古怪,但是它在时间和空间上都是很高效的。
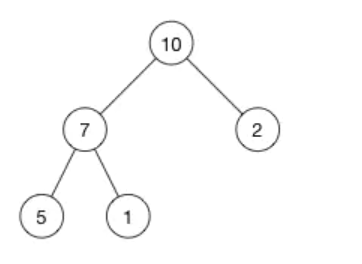
举个例子以下面这个大根堆为例:
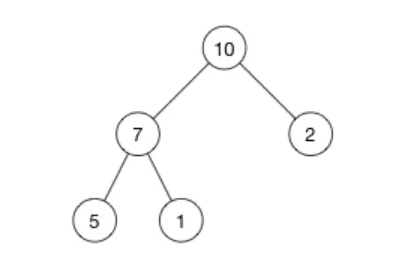
这个数就可以用数组**[ 10, 7, 2, 5, 1 ]来存储。数组实现的堆中,第N个结点的左孩子索引是(2N+1),右孩子的索引是(2N+2)**。
如果 i 是节点的索引,那么下面的公式就给出了它的父节点和子节点在数组中的位置:
- parent(i) = (i-1)/2
- left(i) = 2*i + 1
- right(i) = 2*i + 2
right(i) = left(i) + 1。左右节点总是处于相邻的位置。
在使用这些索引值的时候需要保证是有效的索引值。如果索引值无效,这说明该结点没有父结点(或子结点)
在最大堆中,父节点的值总是要大于(或者等于)其子节点的值。这意味这个公式对数组中任意一个索引 i都成立:array[parent(i)] >= array[i]
分析出了上面这些公式,我们就可以不使用指针就可以找到任何一个节点的父节点或者子节点。事情比简单的去掉指针要复杂,但这就是交易:我们节约了空间,但是要进行更多计算,幸好这些计算很快并且只需要**O(1)**的时间。
理解数组索引和节点位置之间的关系非常重要。这里再给一个最小堆的例子:

注意:图片中的数字不是节点的值,而是存储这个节点的数组索引!数组索引和树的层级之间的关系以及在图中给出了。
还有一个要注意的点,在堆中,在当前层级所有的节点都已经填满之前不允许开始下一层的填充。所以堆总是像这样的形状:

当然可以使用普通树来模拟堆,但是那对空间是极大的浪费。
一个从低到高有序排列的数组是一个有效的最小堆,一个从高到低有序排列的数组是一个有效的最大堆。
我们以数组[ 10, 14, 25, 33, 81, 82, 99 ]为例,将其展开为堆结果如下:

可以发现是一个最小堆。
**注意:**并不是每一个最小堆都是一个有序数组!要将堆转换成有序数组,需要使用堆排序。
最后再补充一个数学公式,根据节点数(数组长度)来求堆的高度。树的高度是指从树的根节点到最低的叶节点所需要的步数,或者更正式的定义:高度是指节点之间的边的最大值。一个高度为 h 的堆有 h+1 层。
举个例子,下面这个对的高度是3,所以它有4层:
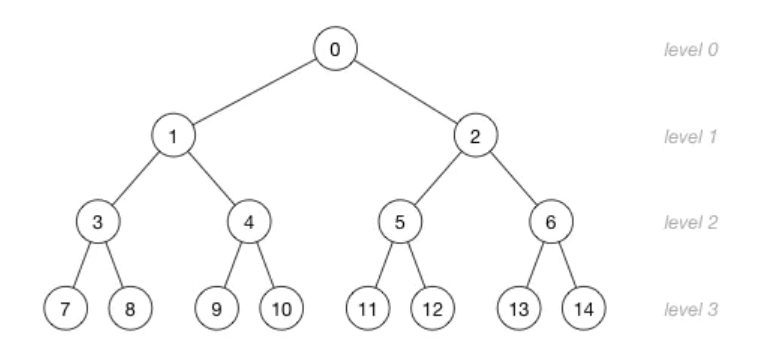
了解了上面这些概念就很好求了,其实就是等比数列前n项和的问题。
堆的相关操作
堆有两个最基本的操作,用于保证插入或删除节点以后堆是一个有效的最大堆或者最小堆:
shiftUp(): 如果一个节点比它的父节点大(最大堆)或者小(最小堆),那么需要将它同父节点交换位置。(即我们之前写过的向上调整算法,代码中有current = parent;)shiftDown(): 如果一个节点比它的子节点小(最大堆)或者大(最小堆),那么需要将它同左孩子交换位置(即我们之前写过的向下调整算法,代码中有current = left;)
shiftUp()和 shiftDown()是一个递归的过程,所以它的时间复杂度是 O(log n)。
基于这两个基本操作就可以实现其他的操作:
insert(value): 在堆的尾部添加一个新的元素,然后使用shiftUp来修复对。remove(): 移除并返回最大值(最大堆)或者最小值(最小堆)。为了将这个节点删除后的空位填补上,需要将最后一个元素移到根节点的位置,然后使用shiftDown方法来修复堆。removeAtIndex(index): 和remove()一样,差别在于可以移除堆中任意节点,而不仅仅是根节点。当它与子节点比较位置无序时使用shiftDown(),如果与父节点比较无序则使用shiftUp()。replace(index, value):将一个更小的值(最小堆)或者更大的值(最大堆)赋值给一个节点。由于这个操作破坏了堆属性,所以需要使用shiftUp()来修复堆属性。
上面所有的操作的时间复杂度都是 O(log n)
下面有一些时间复杂度更高的操作:
search(value):堆不是为快速搜索而建立的,但是replace()和removeAtIndex()操作需要找到节点在数组中的index,所以你需要先找到这个index。时间复杂度:O(n)。buildHeap(array):通过反复调用insert()方法将一个(无序)数组转换成一个堆。如果你足够聪明,你可以在 O(n) 时间内完成。- 堆排序:由于堆就是一个数组,我们可以使用它独特的属性将数组从低到高排序。时间复杂度:O(n lg n)。
堆最重要的功能还是插入和删除根节点,所以主要还是来看一下插入节点和删除根节点。
插入
insert(value): 在堆的尾部添加一个新的元素,然后使用 shiftUp 来修复对。
我们通过一个插入例子来看看插入操作的细节。我们将数字 16 插入到这个最大堆中:

过程如下:
-
首先数组由[ 10, 7, 2, 5, 1 ]变成了[ 10, 7, 2, 5, 1, 16 ],相应的树变成了:
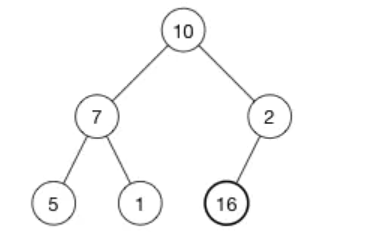
-
由于最大堆的特性,父结点必须要比子结点大,所以
2和16要互换位置:
此时还没有结束,因为
10也比16小。我们继续交换我们的插入元素和它的父节点,直到它的父节点比它大或者我们到达树的顶部。这就是所谓的shiftUp()(向上调整法),每一次插入操作后都需要进行。它将一个太大或者太小的数字“浮起”到树的顶部。、 -
最后我们得到的堆:

数组即变为了:[16,7,10,5,1,2]
删除根节点
remove(): 移除并返回最大值(最大堆)或者最小值(最小堆)。为了将这个节点删除后的空位填补上,需要将最后一个元素移到根节点的位置,然后使用 shiftDown 方法来修复堆。
还是以这个堆为例:

我们将这个树中的 (10) 删除,过程如下:
-
删除根节点后,现在顶部有一个空的节点:

当插入节点的时候,我们将新的值返给数组的尾部。现在我们来做相反的事情:我们取出数组中的最后一个元素,将它放到树的顶部,然后再修复堆属性。如下:

-
接下来就需要进行
shiftDown()操作了,即向下调整法。为了保持最大堆的堆属性,我们需要树的顶部是最大的数据。现在有两个数字可用于交换:7 和 2。我们选择这两者中的较大者为最大值放在树的顶部,所以交换7和1,现在树变成了:
还没有结束,因为5也比1大,所以我们将
5和1也互换位置: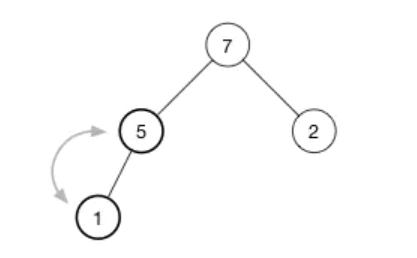
-
这样我们就得到删除根节点后的堆了,数组也由[10, 7, 2, 5, 1]变成了[ 7,5,2,1 ]
删除任意节点
removeAtIndex(index): 和 remove() 一样,差别在于可以移除堆中任意节点,而不仅仅是根节点。当它与子节点比较位置无序时使用 shiftDown(),如果与父节点比较无序则使用 shiftUp()。
在绝大多数时候你需要删除的是堆的根节点,因为这就是堆的设计用途。但是,删除任意节点也很有用。这是 remove() 的通用版本,它可能会使用到 shiftDown() 和 shiftUp()。
还是以上面这个堆为例:
大致思路就是:数组原本为:[10,7,2,5,1],假如要删除7,那么先让7和``1互换位置,数组变为:[10,1,2,5,7],然后删除堆的最后一个元素(即数组的最后一个元素), removeLast() 操作。数组变为了[10,1,2,5],接下来再根据最大堆的特性来选择执行 shiftDown() 和 shiftUp(),最后修复的堆数组为: [10,5,2,1]。
(英文原文)
配对堆
配对堆是一个支持插入,查询/删除最小值,合并,修改元素等操作的数据结构,也就是俗称的可并堆。
配对堆在 OI 界十分的冷门,但其实跑得比较快,也很好写,但不能可持久化,因为配对堆复杂度是势能分析出来的均摊复杂度。
左偏树
左偏树 与 配对堆 一样,是一种 可并堆,具有堆的性质,并且可以快速合并。
堆和优先队列的区别
PriorityQueue(优先队列)和Heap(堆)到底有什么区别?
首先来看名字:
- 优先队列:说到底还是一种队列,不过是一种特殊的队列。它的主要作用就是poll()/peek()出队列中最大/最小的那个元素。
- 堆:首先我们要明确:堆是一个很大的概念,它并不一定是完全二叉树。我们之前用完全二叉树是因为这个很容易被数组储存(index: index * 2是右子节点 index*2+1是左子节点)。正因为这样,所以大部分情况我们用完全二叉树(数组)来储存堆,但是除了这种二叉堆之外,像二项堆、斐波那契堆这种堆就不属于二叉树。
那么优先对列和堆有什么区别呢?这里说的堆默认我们最常使用的二叉堆,而二叉堆只是优先队列的一种是实现方式而已。
那么优先队列还有哪些实现方式呢?二项堆,平衡树,线段树,甚至用二进制分组的vector来实现一个优先对列。
所以说,优先队列和堆不是一个同level的概念,如果非要说,他们之间的关系就是:二叉堆只是优先队列的一种实现方式,而Java的PriorityQueue就是通过用数组表示的小根堆实现的。
散列
哈希表是又称散列表,一种以 “key-value” 形式存储数据的数据结构。所谓以 “key-value” 形式存储数据,是指任意的键值 key 都唯一对应到内存中的某个位置。只需要输入查找的键值,就可以快速地找到其对应的 value。可以把哈希表理解为一种高级的数组,这种数组的下标可以是很大的整数,浮点数,字符串甚至结构体。
关于Java中对哈希表的具体实现,如HashSet,LinkedHashSet,HashMap,LinkedHashMap 之类的,在之前Java数据结构之集合知识全系列的笔记中已经介绍过了。
这里我们以HashMap为例,再具体学习一下。
散列表,是一种数据结构,通过存储位置与key的映射关系存储数据,实现平均时间复杂度为
O(1)的查找功能。在Java中,每个类因为继承关系,都含有一个public int hashCode()方法,当我们要将自己实现的类作为散列表中的key时,我们需要自己重写这个函数。
查找
我们知道在查找一个线性表中是否contains某个值时,我们需要遍历整个线性表,判断是否存在某个值,时间复杂度为O(n),如Java中的ArrayList和LinkedList。
这时候散列表就显示出它的作用来了,它就是为快速查找value诞生的。在Java中HashMap就是散列表的实现,从 jdk1.8开始,HashMap 主要是由数组+单向链表+红黑树 实现,相比 jdk1.7 而言,多了一个红黑树实现。
HashMap 的实现原理,算是面试必问的一个话题,详细的实现过程,有兴趣的朋友可以参考文章【集合系列】- 深入浅出分析HashMap!
hashCode()方法
散列值也即哈希值,提到哈希值,我们不禁会联想到Java里到hashCode()方法与equals()方法。
hashCode()方法返回该对象的哈希码值,在一次Java应用运行期间,如果该对象上equals()方法里比较的信息没有修改,则对该对象多次调用hashCode()方法时返回相同的整数。
从这个定义我们可以了解到以下几点:
- 当
equals()方法被重写时,通常有必要重写hashCode()方法,以维护hashCode()方法的常规协定,该协定声明相等对象必须具有相等的哈希码。 - hashCode的存在主要用来提升查找的快捷性,HashMap、Hashtable等用hashCode来确定散列表中对象的存储地址。
- 两个对象相同,则两个对象的hashCode相同,反过来却不一定,hashCode相同只能说明这两个对象放在散列表里的同一个"篮子"里。
哈希冲突
通过上面的描述,我们可以知道散列表主要面临的问题是散列值均匀的分布,而我们主要解决的问题是在散列值在计算的时候出现的冲突问题,即出现了两个相同的散列值,通常这也成为哈希冲突。
对于发生Hash冲突的情况,冲突有两种实现方式,一种开放地址方式(当发生hash冲突时,就继续以此继续寻找,直到找到没有冲突的hash值),另一种是拉链方式(将冲突的元素放入链表)。Java HashMap采用的就是第二种方式,拉链法。
散列的实现及jdk源码分析
后面再补。
可以参考:深入浅出分析HashMap
并查集
后面学前缀树(Tire Tree)的时候一起补。

