Java数据结构之树
预备知识
树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合。

相关概念
树的结点
-
结点:使用树结构存储的每一个数据元素都被称为“结点”。例如,图 1(A)中,数据元素 A 就是一个结点。
-
父结点(双亲结点)、子结点和兄弟结点:对于图 1(A)中的结点 A、B、C、D 来说,A 是 B、C、D 结点的父结点(也称为“双亲结点”),而 B、C、D 都是 A 结点的子结点(也称“孩子结点”)。对于 B、C、D 来说,它们都有相同的父结点,所以它们互为兄弟结点。
-
树根结点(简称“根结点”):每一个非空树都有且只有一个被称为根的结点。图 1(A)中,结点A就是整棵树的根结点。
树根的判断依据为:如果一个结点没有父结点,那么这个结点就是整棵树的根结点。
-
叶子结点:如果结点没有任何子结点,那么此结点称为叶子结点(叶结点)。例如图 1(A)中,结点 K、L、F、G、M、I、J 都是这棵树的叶子结点。
子树和空树
-
子树:如图 1(A)中,整棵树的根结点为结点 A,而如果单看结点 B、E、F、K、L 组成的部分来说,也是棵树,而且节点 B 为这棵树的根结点。所以称 B、E、F、K、L 这几个结点组成的树为整棵树的子树;同样,结点 E、K、L 构成的也是一棵子树,根结点为 E。
注意:单个结点也是一棵树,只不过根结点就是它本身。图 1(A)中,结点 K、L、F 等都是树,且都是整棵树的子树。
知道了子树的概念后,树也可以这样定义:树是由根结点和若干棵子树构成的。
补充:**在树结构中,对于具有同一个根结点的各个子树,相互之间不能有交集。**例如,图 1(A)中,除了根结点 A,其余元素又各自构成了三个子树,根结点分别为 B、C、D,这三个子树相互之间没有相同的结点。如果有,就破坏了树的结构,不能算做是一棵树。
-
空树:如果集合本身为空,那么构成的树就被称为空树。空树中没有结点。
结点的度和层次
-
结点的度:对于一个结点,拥有的子树数(结点有多少分支)称为结点的度(Degree)。例如,图 1(A)中,根结点 A 下分出了 3 个子树,所以,结点 A 的度为 3。
一棵树的度是树内各结点的度的最大值。图 1(A)表示的树中,各个结点的度的最大值为 3,所以,整棵树的度的值是 3。
-
结点的层次:**从一棵树的树根开始,树根所在层为第一层,根的孩子结点所在的层为第二层,依次类推。**对于图 1(A)来说,A 结点在第一层,B、C、D 为第二层,E、F、G、H、I、J 在第三层,K、L、M 在第四层。
**一棵树的深度(高度)是树中结点所在的最大的层次。**图 1(A)树的深度为 4。
如果两个结点的父结点虽不相同,但是它们的父结点处在同一层次上,那么这两个结点互为堂兄弟。例如,图 1(A)中,结点 G 和 E、F、H、I、J 的父结点都在第二层,所以之间为堂兄弟的关系。
有序树和无序树
如果树中结点的子树从左到右看,谁在左边,谁在右边,是有规定的,这棵树称为有序树;反之称为无序树。
在有序树中,一个结点最左边的子树称为"第一个孩子",最右边的子树称为"最后一个孩子"。拿图 1(A)来说,如果是其本身是一棵有序树,则以结点 B 为根结点的子树为整棵树的第一个孩子,以结点 D 为根结点的子树为整棵树的最后一个孩子。
森林
由 m(m >= 0)个互不相交的树组成的集合被称为森林。图 1(A)中,分别以 B、C、D 为根结点的三棵子树就可以称为森林。
前面讲到,树可以理解为是由根结点和若干子树构成的,而这若干子树本身是一个森林,所以,树还可以理解为是由根结点和森林组成的。用一个式子表示为:
1 | Tree =(root,F) |
其中,root 表示树的根结点,F 表示由 m(m >= 0)棵树组成的森林。
树的表示方法
除了图 1(A)表示树的方法外,还有其他表示方法:
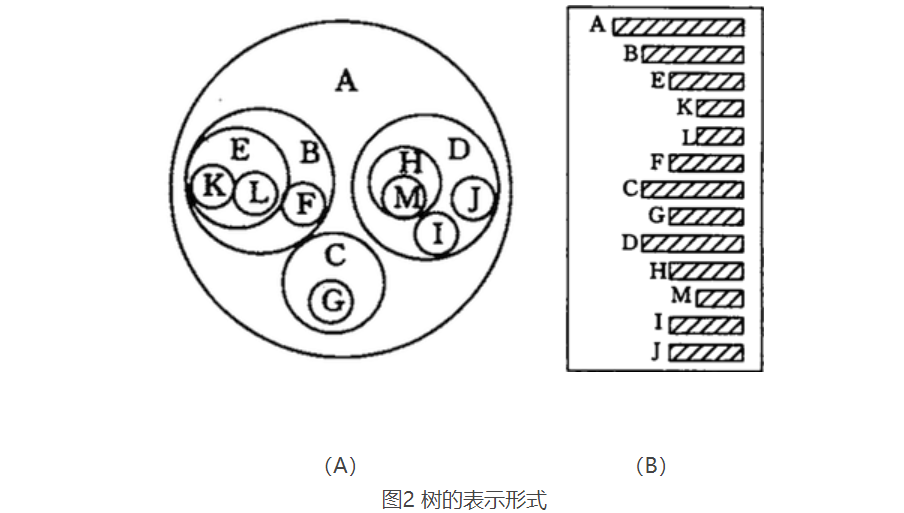
-
图 2(A)是以嵌套的集合的形式表示的(集合之间绝不能相交,即图中任意两个圈不能相交)
-
图 2(B)使用的是凹入表示法(了解即可),表示方式是:最长条为根结点,相同长度的表示在同一层次。例如 B、C、D 长度相同,都为 A 的子结点,E 和 F 长度相同,为 B 的子结点,K 和 L 长度相同,为 E 的子结点,依此类推
-
最常用的表示方法是使用**广义表**的方式。图 1(A)用广义表表示为:
1
(A , ( B ( E ( K , L ) , F ) , C ( G ) , D ( H ( M ) , I , J ) ) )
最后说一下树结构(一对多)和之前的线性结构的区别:
| 树结构 | 线性结构 |
|---|---|
| 根结点:无双亲,唯一 | 第一个数据元素:无前驱元素 |
| 叶结点:无孩子,可以多个 | 最后一个元素:无后继元素 |
| 中间结点:一个双亲多个孩子 | 中间元素:一个前驱元素一个后继元素 |
存储普通树的方法
大概分为三种:
- 双亲表示法
- 孩子表示法
- 孩子兄弟表示法(孩子兄弟表示法可以作为将普通树转化为二叉树的最有效方法,通常又被称为"二叉树表示法"或"二叉链表表示法")
这里就先不给代码了,参考资料:树的双亲表示法(C语言实现详解版)
二叉树
接下来我们来学习一下一类具体的树结构:二叉树。
满足以下两个条件的树就是二叉树:
- 本身是有序树
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2

二叉树性质
二叉树性质如下:
-
二叉树中,第 i 层最多有 2^(i-1) 个结点(很好理解,2的i-1次方嘛)
-
如果二叉树的深度为 K,那么此二叉树最多有 2^K-1 个结点(等比数列之和即可求出)
-
二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1
性质 3 的计算方法为:对于一个二叉树来说,除了度为 0 的叶子结点和度为 2 的结点,剩下的就是度为 1 的结点(设为 n1),那么总结点 n=n0+n1+n2。
同时,对于每一个结点来说都是由其父结点分支表示的,假设树中分枝数为 B,那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的,即 B=n1+2n2。所以,n 用另外一种方式表示为 n=n1+2n2+1。
两种方式得到的 n 值组成一个方程组,就可以得出 n0=n2+1。
二叉树分类
二叉树又可以分为满二叉树和完全二叉树。也有一种特殊的二叉树叫做二叉查找树。
满二叉树
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。

满二叉树除了满足普通二叉树的性质,还具有以下性质:
- 满二叉树中第 i 层的节点数为 2^(n-1)个(2的i-1次方)
- 深度为 k 的满二叉树必有 2^k-1 个节点 ,叶子数为 2^k-1(等比数列前n项和)
- 满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层
- 具有 n 个节点的满二叉树的深度为㏒₂n+1
完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
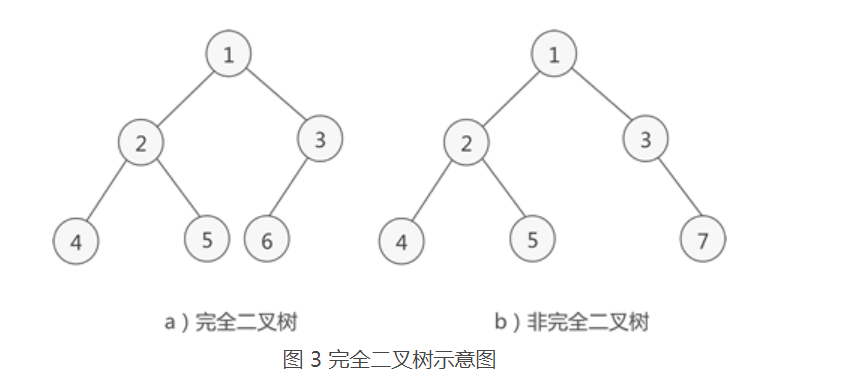
(如图所示,a是一棵完全二叉树,而b由于最后一层的节点没有按照从左向右分布,因此只能算作是普通的二叉树)
完全二叉树除了具有普通二叉树的性质,它自身也具有一些独特的性质,比如说,n 个结点的完全二叉树的深度为 ⌊㏒₂n⌋+1。
⌊㏒₂n⌋ 表示取小于㏒₂n 的最大整数。例如,⌊log24⌋ = 2,而 ⌊log25⌋ 结果也是 2。
对于任意一个完全二叉树来说,如果将含有的结点按照层次从左到右依次标号(如图 3a)),对于任意一个结点 i ,完全二叉树还有以下几个结论成立:
- 当 i>1 时,父亲结点为结点 [i/2] 。(i=1 时,表示的是根结点,无父亲结点)
- 如果 2i>n(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 2i
- 如果 2i+1>n ,则结点 i 肯定没有右孩子;否则右孩子是结点 2i+1
二叉查找树
二叉查找树(BST:Binary Search Tree)是一种特殊的二叉树,它改善了二叉树节点查找的效率。二叉查找树有以下性质,对于任意一个节点 node:
- 其左子树(left subtree)下的每个后代节点(descendant node)的值都小于节点 n 的值
- 其右子树(right subtree)下的每个后代节点的值都大于节点 n 的值
简言之,就是左<中<右。
下图中,a为普通二叉树,b是二叉查找树。

二叉树的遍历
二叉树的遍历主要分三种:
- 先序遍历
- 中序遍历
- 后序遍历
第四种也有二叉树的层次遍历。
二叉树遍历的代码实现我们会在下面的二叉树实现中给出,这里先介绍一下这四种遍历。
先序遍历
二叉树先序遍历的实现思想是:
- 访问根节点
- 访问当前节点的左子树
- 若当前节点无左子树,则访问当前节点的右子树
以图 1 为例,采用先序遍历的思想遍历该二叉树的过程为:
- 访问该二叉树的根节点,找到 1
- 访问节点 1 的左子树,找到节点 2
- 访问节点 2 的左子树,找到节点 4
- 由于访问节点 4 左子树失败,且也没有右子树,因此以节点 4 为根节点的子树遍历完成。但节点 2 还没有遍历其右子树,因此现在开始遍历,即访问节点 5
- 由于节点 5 无左右子树,因此节点 5 遍历完成,并且由此以节点 2 为根节点的子树也遍历完成。现在回到节点 1 ,并开始遍历该节点的右子树,即访问节点 3
- 访问节点 3 左子树,找到节点 6
- 由于节点 6 无左右子树,因此节点 6 遍历完成,回到节点 3 并遍历其右子树,找到节点 7;
- 节点 7 无左右子树,因此以节点 3 为根节点的子树遍历完成,同时回归节点 1。由于节点 1 的左右子树全部遍历完成,因此整个二叉树遍历完成
因此,该二叉树的先序遍历结果为:1,2,4,5,3,6,7
中序遍历
二叉树中序遍历的实现思想是,从根节点出发:
- 访问当前节点的左子树
- 访问根节点
- 访问当前节点的右子树
以图 1 为例,采用中序遍历的思想遍历该二叉树的过程为:
- 访问该二叉树的根节点,找到 1
- 遍历节点 1 的左子树,找到节点 2
- 遍历节点 2 的左子树,找到节点 4
- 由于节点 4 无左孩子,因此找到节点 4,并遍历节点 4 的右子树
- 由于节点 4 无右子树,因此
节点 2 的左子树遍历完成,输出节点4,访问节点 2,输出节点2- 遍历节点 2 的右子树,找到节点5,输出节点5
- 由于节点 5 无左子树,因此访问节点 5 ,又因为节点 5 没有右子树,因此
节点 1 的左子树遍历完成,访问节点 1 ,输出节点1,并遍历节点 1 的右子树,找到节点 3;- 遍历节点 3 的左子树,找到节点 6
- 由于节点 6 无左子树,因此访问节点 6,输出节点6,又因为该节点无右子树,因此
节点 3 的左子树遍历完成,开始访问节点 3 ,输出节点3,并遍历节点 3 的右子树,找到节点 7- 由于节点 7 无左子树,因此访问节点 7,输出节点7,又因为该节点无右子树,因此
节点 1 的右子树遍历完成,即整棵树遍历完成因此,该二叉树的中序遍历结果为:4,2,5,1,6,3,7
后序遍历
二叉树后序遍历的实现思想是:从根节点出发:
- 访问当前节点的左子树
- 访问当前节点的右子树
- 访问根节点
(从根节点出发,依次遍历各节点的左右子树,直到当前节点左右子树遍历完成后,才访问该节点元素)
如图 1 中,对此二叉树进行后序遍历的操作过程为:
- 从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点)
- 遍历节点 2 的左子树(以节点 4 为根节点)
- 由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍历节点 2 的右子树(以 5 为根节点)
- 由于节点 5 无左右子树,因此可以访问节点 5 ,并且此时节点 2 的左右子树也遍历完成,因此也可以访问节点 2
- 此时回退到节点 1 ,开始遍历节点 1 的右子树(以节点 3 为根节点)
- 遍历节点 3 的左子树(以节点 6 为根节点)
- 由于节点 6 无左右树,因此访问节点 6,并回退到节点 3,开始遍历节点 3 的右子树(以节点 7 为根节点)
- 由于节点 7 无左右子树,因此访问节点 7,并且节点 3 的左右子树也遍历完成,可以访问节点 3;节点 1 的左右子树也遍历完成,可以访问节点 1
- 到此,整棵树的遍历结束
因此,该二叉树的后序遍历结果为:4,5,2,6,7,3,1
层次遍历
如下图所示为二叉树的层次遍历,即按照箭头所指方向,按照1、2、3、4的层次顺序,对二叉树中各个结点进行访问(此图反映的是自左至右的层次遍历,自右至左的方式类似)。

二叉树层次遍历的实现逻辑:要建立一个队列。先将二叉树头结点入队列,然后出队列,访问该结点,如果它有左子树,则将左子树的根结点入队:如果它有右子树,则将右子树的根结点入队。然后出队列,对出队结点访问,如此反复,直到队列为空为止。(其实也可以用栈来实现,画一下图逻辑就能理解了)
代码我们写在下面的二叉树实现中。
二叉树的实现
- 二叉树的顺序存储,指的是使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树(注意满二叉树也是完全二叉树)
- 二叉树的链式存储结构更适合用来存储二叉树。二叉树并不适合用数组存储,因为并不是每个二叉树都是完全二叉树,普通二叉树使用顺序表存储或多或多会存在空间浪费的现象
我们使用链式存储结构来实现二叉树。在之前的学习中我们已经谁了节点类Node的使用。在这里我们也要创建一个节点类BinaryTreeNode,它的属性有:
- 节点存储的数据(data)
- 指向左孩子节点的指针(leftChild)
- 指向右孩子节点的指针(rightChild)
像我们这种,在一个节点中存储了两个个指针域的链表结构,通常称为二叉链表。有的二叉树实现使用三叉链表实现:即除了存储指向左孩子节点的指针(leftChild)和指向右孩子节点的指针(rightChild),还有存储指向父节点的指针(parentChild)。在解决实际问题时,用合适的链表结构存储二叉树,可以起到事半功倍的效果。
二叉树结点
首先我们要先创建一个二叉树结点类BinaryTreeNode,代码如下:
1 | /** |
二叉树
然后创建二叉树类BinaryTree,代码如下:
1 | /** |
二叉树的四种遍历
关于二叉树遍历的四种实现,我们专门在下面列出。代码如下:
1 | /** |
二叉搜索树(BST)
平衡二叉树(AVL)
红黑树(R-B Tree)
哈夫曼树(Huffman Tree)
哈夫曼树,也叫最优二叉树。
相关概念

- 路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。图 1 中,从根结点到结点 a 之间的通路就是一条路径。
- 路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。图 1 中从根结点到结点 c 的路径长度为 3。
- 结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。例如,图 1 中结点 a 的权为 7,结点 b 的权为 5。
- 结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如,图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。
- 树的带权路径长度:树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为:WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3
什么是哈夫曼树
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。
在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。在图 1 中,因为结点 a 的权值最大,所以理应直接作为根结点的孩子结点。
构建哈夫曼树
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
- 在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
- 在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
- 重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树。

图 2 中,(A)给定了四个结点a,b,c,d,权值分别为7,5,2,4;第一步如(B)所示,找出现有权值中最小的两个,2 和 4 ,相应的结点 c 和 d 构建一个新的二叉树,树根的权值为 2 + 4 = 6,同时将原有权值中的 2 和 4 删掉,将新的权值 6 加入;进入(C),重复之前的步骤。直到(D)中,所有的结点构建成了一个全新的二叉树,这就是哈夫曼树。
哈夫曼编码
哈夫曼编码就是在哈夫曼树的基础上构建的,这种编码方式最大的优点就是用最少的字符包含最多的信息内容。
根据发送信息的内容,通过统计文本中相同字符的个数作为每个字符的权值,建立哈夫曼树。对于树中的每一个子树,统一规定其左孩子标记为 0 ,右孩子标记为 1 。这样,用到哪个字符时,从哈夫曼树的根结点开始,依次写出经过结点的标记,最终得到的就是该结点的哈夫曼编码。
文本中字符出现的次数越多,权值越大,在哈夫曼树中的体现就是越接近树根。编码的长度越短。

如图 3 所示,字符 a 用到的次数最多,其次是字符 b 。字符 a 在哈夫曼编码是 0 ,字符 b 编码为 10 ,字符 c 的编码为 110 ,字符 d 的编码为 111 。
哈夫曼树的实现
构建哈夫曼树时,首先需要确定树中结点的构成。由于哈夫曼树的构建是从叶子结点开始,不断地构建新的父结点,直至树根,所以结点中应包含指向父结点的指针。但是在使用哈夫曼树时是从树根开始,根据需求遍历树中的结点,因此每个结点需要有指向其左孩子和右孩子的指针。(即使用三叉链表)
这里在实现二叉树时,用到了最小堆(又叫小根堆)。(其实可以使用Java中的优先队列 PriorityQueue来实现,不需要自己再写一个最小堆,但是这里我们顺带学习一下最小堆就手写了一个)
和实现二叉树一样,在实现哈夫曼树之前我们先来看看哈夫曼树结点类:
- key:结点的权值
- left:结点的左孩子
- right:结点的右孩子
- parent:结点的父结点
哈夫曼树结点
首先创建哈夫曼树结点类HuffmanNode,代码如下:
1 | /** |
哈夫曼树
然后创建HuffmanTree类,代码如下:
1 | import java.util.ArrayDeque; |
这里关键的其实就是哈夫曼树的创建过程。根据哈夫曼树的特性很容易想到用升序优先队列(最小堆或者叫小根堆)来实现。
以数组{5,6,8,7,15}为例,哈夫曼树的构造过程如下:

最小堆(升序优先队列)
其中最小堆其实可以用Java自带的优先队列来实现,这里我们敲一下代码体会下如何实现优先队列。代码如下:
1 | import java.util.ArrayList; |
前缀树(Tire Tree)
伸展树
B树
标准库中的集合与映射
在之前的笔记中我们讨论过的List容器,即ArrayList和LinkedList用于查找效率很低。因此,Collections API提供了两个附加容器Set和Map,它们对诸如插人、删除和查找等基本操作提供有效的实现。
在 Java 中,集合大致可以分为两大体系,一个是 Collection,另一个是 Map,都位于
java.util包下。
- Collection :主要由 List、Set、Queue 接口组成,List 代表有序、重复的集合;其中 Set 代表无序、不可重复的集合;Java 5 又增加了 Queue 体系集合,代表队列集合。
- Map:则代表具有映射关系的键值对集合。
java.util.Collection下的接口和继承类关系简易结构图:
java.util.Map下的接口和继承类关系简易结构图:
在 Java 集合框架中,数据结构和算法可以说在里面体现的淋淋尽致,这一点可以从我们之前对各个集合类的分析就可以看的出来,如动态数组、链表、红黑树、Set、Map、队列、栈、堆等,基本上只要出去面试,集合框架的话题一定不会少!
更具体的,可参考我搬运的笔记:Java数据结构之集合知识全系列